[2009개정 6학년 1학기 수학] 2. 분수와 소수의 나눗셈 03-04
2. 분수와 소수의 나눗셈
03 나눗셈 문제 만들기
지난 시간에는 나눗셈 의미를 공부하여 보았습니다. 나눗셈은 기본적으로 등분제와 포함제 맥락이 담겨 있는 연산입니다.
등분제는, 한 사람에게 돌아가는 몫에 대한 이야기입니다. 나눗셈은 기본적으로 몫을 구하는 의미를 가지고 있습니다. 예를 들어,
귤 여섯 개를 두 사람에게 나누어 줄 때, 한 사람이 몇 개의 귤을 가집니까?
라는 문제가 있을 때, 나눗셈 식은
6÷2
라고 세우게 되는데, 이 때 구해지는 값은 3이고, 이 값은 한 사람에게 돌아가는 귤의 수, 즉 몫이 됩니다.
포함제는, 전체 양이 몇 번에 걸쳐 나누어지는가에 대한 이야기입니다. 어찌보면, 뺄셈의 의미를 가진 식이라고 볼 수도 있습니다. 예를 들어,
귤 여섯 개를 두 개씩 나누어 줄 때, 몇 사람에게 나누어 줄 수 있습니까?
라는 문제가 있을 때, 나눗셈 식은 위의 등분제와 같이,
6÷2
라고 세우게 되고 이 때 구해지는 답도 3이 되지만, 이 값은 한 사람에게 돌아가는 몫이 이미 정해져 있는 상태에서 몇 번이나 나누어 질 수 있는가를 물어보는 의미가 있다고 할 수 있습니다.
뺄셈과의 연관성은, 결국 6에서 2씩 몇 번 빼어내는가, 즉,
6-2-2-2=0
에서, 2를 세 번 빼어내니까, 귤은 세 사람에게 돌아갈 수 있다, 고 해도 무방한 문제가 된다는 의미입니다. 그렇게보니, 덧셈의 의미를 곱셈이 담고 있는 것처럼, 뺄셈의 의미를 나눗셈이 담고 있다고 볼 수도 있는 것이죠.
한 걸음 더 나아가, 나눗셈은 곱셈식의 역산으로써의 쓰임도 있다고 할 수도 있습니다. 예를 들어,
재석이는 두 개의 귤을 가지고 있고, 형돈이는 여섯 개의 귤을 가지고있을 때, 형돈이는 재석이가 가진 귤의 몇 배만큼 가지고 있는가?
라고 할 때의 문제를, 나눗셈 식으로,
6÷2
로 나타낼 수도 있지만,
2×□=6
으로 표시하여 □안의 값을 구할 수도 있는 것이죠. 이 때의 나눗셈은 곱셈의 역산으로써의 의미를 가질 수도 있다고 봅니다.
아이들에게 이와 같은 바를 다시 한 번 상기시킨 후, 아이들이 나눗셈의 의미가 담긴 다양한 문제를 만들어보도록 하는 활동을 해 보았습니다.
아래는 아이들의 활동 모습.






활동이 끝난 뒤, 각자의 나눗셈 의미가 담긴 문제를 모둠별로 살펴본 후, 이 중 친구들에게 가장 추천하고 싶은 문제 하나를 모둠별로 골라 써 보도록 하였습니다.


그런 다음, 개인의 문제는 개인별로 나와서 붙여보도록 하였습니다. 자신이 생각할 때, 비슷한 의미가 담긴 나눗셈 문제끼리 모아 붙이도록 하였는데, 이러면서 다른 친구들의 문제도 살펴볼 수 있습니다.
그런 후에, 본격적으로 한 번 씩 나와서 자유롭게 읽어보도록 하기도 하였습니다.
붙이기 활동이 끝난 후, 제가 직접 아이들의 문제를 하나하나 살펴보면서, 문제의 분류를 다시 해 보는 일을 도우면서, 나눗셈 의미를 되짚어 보았습니다.
그런 다음, 각 모둠별로 선정한 문제들도 살펴보았습니다.

아래는 문제들.

위 문제는 등분제 의미의 문제입니다. 그런데... 사탕을 8/10명에게 나누어준다고 하였죠. 사람은 분수로 나타낼 수 없습니다. 그런 이야기도 해 주었습니다.

위 문제는, 분수 나눗셈 식이 나옵니다. 그런데... 연필 2/13자루 같은 의미는 우리가 실제 사용하는 수 맥락이라고 할 수는 없겠지요. 그런 이야기도 당연히 해 주었습니다.

이 문제도, 곰곰히 생각해보면 말이 되지 않습니다. 4/12cm를 8cm씩 나눌 수 없습니다. 나눗셈으로 풀 수야 있지만, 실제 맥락이 될 수 없는 문제들이 아이들에게서 쉽게 나옵니다.
그래서 나눗셈 문제가 어렵습니다. 문제의 이해도 쉽지 않고, 맥락을 맞추기도 어렵습니다. 그리고 이런 상태에서 나눗셈 문제를 참 기계적으로 풀어내고 있지 않는가라는 생각이 들었습니다.
그리고... 위의 문제들이 아이들이 뽑은, 각 모둠별로 가장 좋은 문제입니다. 참 어려운 일입니다.

위 문제는 등분제 의미의 나눗셈. 분수/소수의 나눗셈은 등분제의 의미를 담기가 어렵습니다. 위 문제도 자연수 범위에서의 문제이죠.

위 문제는 문제집에 주로 나오는 형식의 문제입니다. 한 문제처럼 보이지만, 실제로는 나눗셈 문제가 두 문제 얽혀있지요. 맥락을 담고 있는 문제는 아니고, 그냥 나눗셈 식 만으로 이루어진 문제입니다.
풀이는, 나눗셈의 곱셈 역산 성질을 이용하여 푼 후, 소수의 나눗셈으로 풉니다. 아직 분수의 나눗셈과 소수의 나눗셈을 본격적으로 배우지는 않았기 때문에, 식으로 풀어보진 않았습니다.

이 문제야말로, 나눗셈이 곱셈 역산의 성질을 가지고 있는 전형적인 문제이며, 또 배움이 필요한 문제입니다. 이런 문제 때문에, 나눗셈의 의미를 등분제와 포함제로만 지도하는 것이 과연 의미있는가를 고민해보게 됩니다.

전형적인 포함제 식의 나눗셈. 뺄셈의 의미가 담겨있는 문제이죠.
위와 같이 활동한 후, 배움을 정리한 아이들의 배움일지.





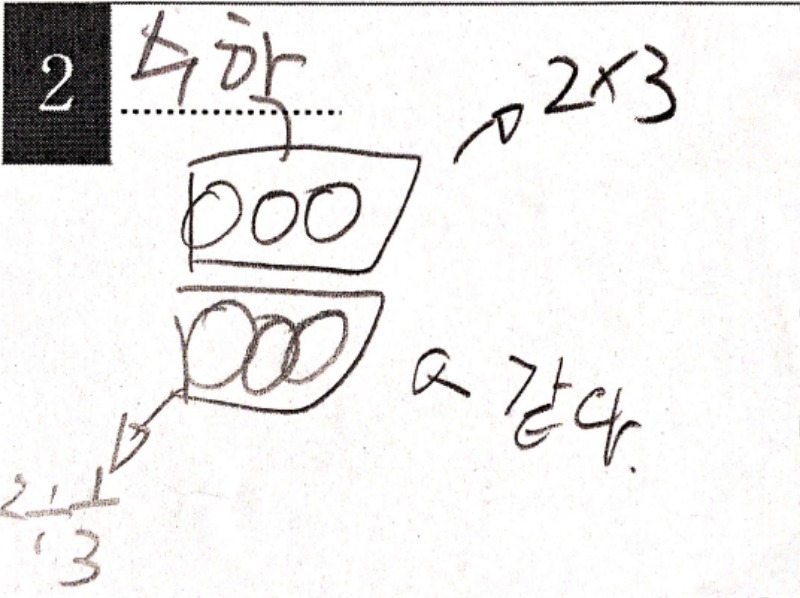


나눗셈의 의미를 한 번 꼼꼼하게 살펴보았으니, 다음 시간에는 이제 이 의미를 가지고 어떻게 문제를 풀어가는지 그 방법에 대한 이야기를 해보기로 하였습니다.
아에드 인 마이오렘 델 글로인

