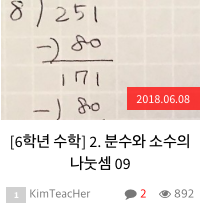
[6학년 수학] 3. 나눗셈 - 나눗셈 세로셈 방법

나눗셈은 개개인에게 돌아갈 똑같은 몫을 구하는 것

여섯 개의 귤을 두 사람에게 똑같게 나누어주면, 과 같은 상황부터

나누어주고 난 후 남는 것이 나오는 상황으로 확장됩니다.

 

그러다가 점점 다루는 수의 범위가 확장되는 방식으로 문제 상황이 주어집니다. 학생들은 문제 상황을 추상화된 식과 기호로 나타내는 방식을 연습하게 되고, 식과 기호를 해결하는 방법을 연습하게 됩니다.

그런데 수의 범위가 확장되면서 어떤 아이들은 큰 어려움에 봉착합니다.

여섯 개의 귤을 두 사람에게 똑같이 나누어주는 상황

은,

6÷2=3

또는

2×3=6

같은 방식으로라도 생각할 수 있는데,

973m의 끈을 47m씩 나누어 가지면 몇 사람이 나누어 가지는가

같은 상황을 해결하지 못하는 학생들이 생겨납니다. 문제 상황을 추상화된 식과 기호로 바꾸어내지 못하는 아이들이 있습니다. 특히 나눗셈 상황을 해결하기 위해 곱셈 사고를 하는 학생들에게는 큰 어려움이 있습니다. 모든 아이들이 여섯 개의 귤을 두 사람에게 나누기 위하여 6 나누기 2의 식을 떠올리는 것은 아니라는 말입니다. 따라서 초등학교 3학년, 4학년 아이들에게 이런 문제를 해결하기 위한 나눗셈 식을 생각해내라는 것을 당연하게 받아들이는 것에는 문제가 있습니다. 교육과정은 평균적이고, 아이들은 개개인의 편차가 존재한다는 것을 교사와 학부모는 이해해야합니다. 어떻게 해야 할까요?

 

교육과정의 재구조화도 필요하겠지만, 리마인드 과정이 반드시 필요하다고 생각합니다. 6학년 아이들이, 나눗셈을 다시 한 번 되짚어 볼 수 있도록 단원을 구성해야 합니다. 그렇지 않으면 초등학교 3, 4학년 때부터 계속 수학포기자는 생겨나게 되고, 이 아이들은 누적되어갑니다. 아이들의 사고를 돕는 수학, 생각하는 힘을 길러주는 수학의 재미와 묘미를 알려주려면, 우선 아이들이 놓치고 있는 부분을 채워주려는 노력이 교실로부터 시작되어야 합니다. 어쨌든.

 

973m의 끈을 47m씩 나누어 가지기 위해서는 이제 이 문제 상황을 나눗셈 식으로 나타내야 합니다.

973÷47

을 과연 어떻게 풀어야 할까요?

 

그래서 아이들에게 나눗셈의 세로셈 알고리즘을 제안합니다. 아이들이 수학이라는 과목을 배우면서 만나는 첫 알고리즘이자 가장 효율적인 알고리즘. 그런데 과연 아이들에게 이 알고리즘의 도입이 효과적이고 적절할까요? 학교 현장에서 생각보다 이 알고리즘의 의미를 제대로 알지 못하는 학생들이 있습니다. 아래는 저희 반 아이들의 나눗셈 알고리즘 사용을 전수조사하여 살펴본, 알고리즘을 잘못 사용하고 있는 예시.

 

 

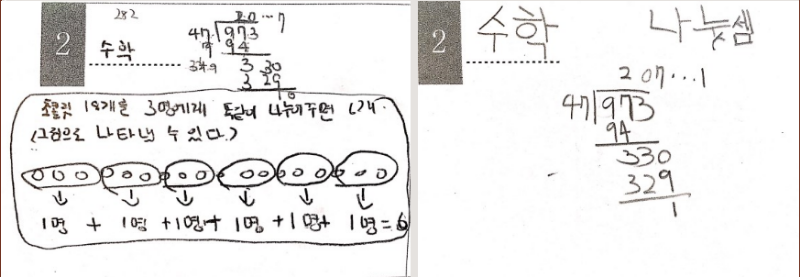
위 아이들은 '그냥 나눠봐라'라고 해서 아마 자연수 범위까지 나누어야 하는지 소수 첫째 자리까지 나누어야 하는지 계속 나누어야 하는지 모호한 덕에 발생한 실수라고 봅니다.

 

 

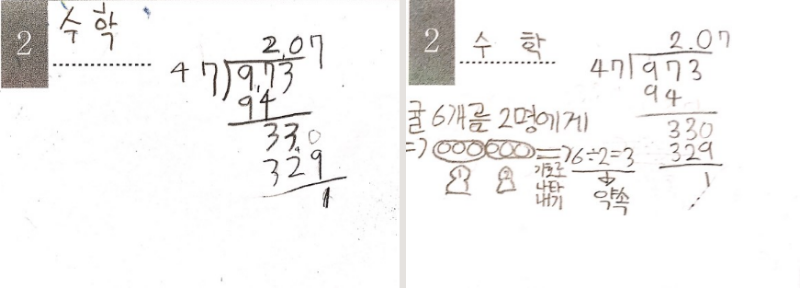
위 아이들은 소수점을 제대로 처리하지 못하여 벌어진 문제입니다. 자연수 범위에서의 나눗셈이지만, 몫의 범위가 확장되면서 아이들은 혼란에 빠져들기도 합니다. 

 

 

 

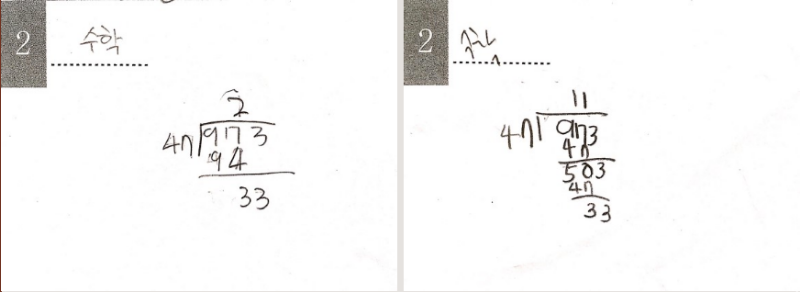
진짜 문제는 위 오른쪽의 아이. 이렇게 이해하지 못한 알고리즘의 사용이 누적되면 이제 조금씩 수학으로부터 멀어지는 결과를 낳을 뿐입니다. 올해 저희 반 아이들은 다행히 나눗셈 세로셈 알고리즘을 곧잘 사용하는 모습을 볼 수 있습니다. 그러나 작년에는 아니었지요. 

 

왜 나눗셈의 세로셈 알고리즘을 도입하는지에 대한 설명이 반드시 주어져야 합니다.

973을 47로 나눈다는 의미는 무엇일까요? 973에서 47씩 몇 번이나 빼 낼 수 있는가의 의미입니다. 나눗셈의 기본 의미는 뺄셈에서 비롯됩니다. 그런데,

6-2-2-2 (2를 세 번 뺀다)

는 쉽지만,

973-47-47-47-47-47-47-47-47-47-47-······

은 쉽지 않습니다.

그래서, 4학년 때 십진기수법을 배우면 아이들은 명확하게 아래와 같이 뺍니다.

973-470=503 (47을 한 번에 열 번 뺀다)

남은 수로부터 또 열 번 빼 낼 수 있습니다.

503-470=33

이렇게 스무 번 빼내는 것을, 아이들은 나눗셈의 세로셈 알고리즘을 이용하여 조금 더 쉽게 나누어 내게 됩니다. 즉,

 

 

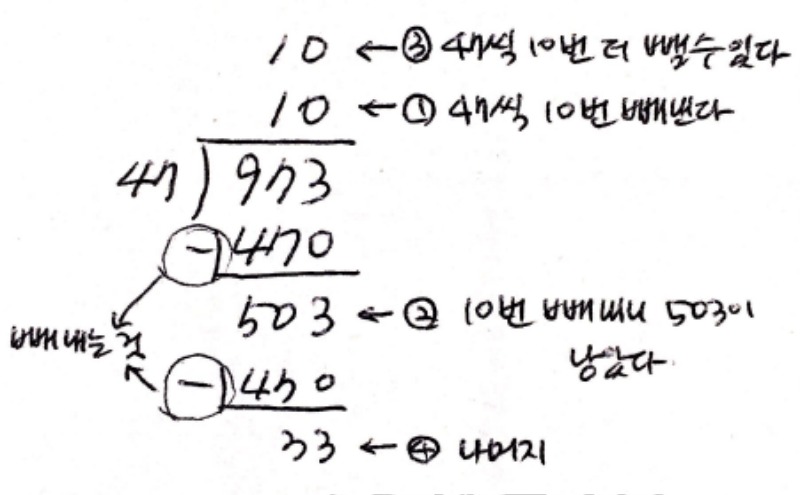
위 뺄셈 사고를 편하게 옮겨 놓은 것이 나눗셈의 세로셈 알고리즘이라고 할 수 있습니다. 우린 이러한 알고리즘을 명확하게 이해시킨 후 안내한다기 보다는 그저 방법으로 제시할 뿐입니다.

 

 

결국 나눗셈의 세로셈 알고리즘을 도입하기 위해서,

 

1. 주어진 문제 상황이 나눗셈 문제 상황임을 안다.

2. 나눗셈 문제 상황을 나눗셈 식으로 표현한다.

3. 표현한 나눗셈 식의 값(몫)을 구하는 것이 뺄셈식 사고가 필요함을 안다.

4. 뺄셈식 사고를 간편하게 나눗셈의 세로셈 알고리즘으로 도입할 수 있다.

 

와 같은 과정을 거치게 되는데, 우리 아이들은 주어진 문제 상황이 나눗셈 문제 상황임을 충분히 생각해 볼 과정도 거치지 못하고, 나눗셈 문제 상황을 나눗셈 식으로 표현하기 위하여 생각할 시간도 갖지 못하며, 나눗셈의 세로셈 알고리즘이 가지고 있는 의미도 충분히 생각할 기회를 갖지 못합니다.

 

이 부분이 명확하게 연습이 된 후에야, 아이들은 자연수 범위에서 다루던 수 범위를 확장하여 소수 범위까지 수를 확장하여 다룰 수 있게 됩니다.

실제수업.

 

확장된 상황

캬라멜 스물 두 개를 네 개 씩 나누어 주면 몇 사람이 캬라멜을 받을까?

상황이 나눗셈 상황임을 확인하기

나눗셈 상황을 식으로 바꾸기

22÷4

 

나눗셈 상황이 결국 뺄셈 상황임을 알기

22-4-4-4-4-4=2 (4를 다섯 번 빼내는 것)

 

나눗셈 상황의 수가 커질 때 해결할 수 있는 방법 확인하기

나눗셈의 세로셈 방법

 

나눗셈의 세로셈 방법이 뺄셈 상황을 확장한 것임을 확인하기

 

실제로 나눗셈의 세로셈 방법으로 풀어보기

 

 

아에드 인 마이오렘 델 글로인