[6학년 수학] 10. 나눗셈(09)-덧셈적 사고와 곱셈적 사고

 

아이들이

 

 

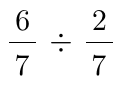
를 해결하기 위해서 왜,

 

  

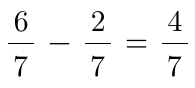
의 풀이를 이용할까요?

  



우선, 아이들이 이런 방식의 사고를 펼칠 기회가 없는 부분부터 이야기를 해야 할 듯 합니다.

 

아이들의 사고는 기존의 경험을 토대로 할 때가 많다고 합니다. 기존에 배웠던 것을 바탕으로 새로운 것을 받아들이는 것. 피아제는 이를 동화와 조절의 과정이라고 설명하고 있습니다. 사실 피아제는 유아의 발달을 동화와 조절의 개념으로 설명하지만, 이는 어른들도 크게 다르지 않습니다. 어른들도 인생 내내 자신의 경험을 토대로 새로운 현상을 설명하고 이해하려는 시도를 하지 않습니까. '라떼는 말이야~'

 

그러나 초등학교 수학 학습 과정에서, 우리 아이들의 배움에는 사전 과정이 없습니다. 왜 그런가 묻긴 하겠지요. 하지만, 그에 대한 충분한 대답을 듣지는 않고 있습니다. 저도 왜 그런지 잠깐 묻고는, 금새 설명해주기에만 바빴던 경험만 가지고 있습니다. 저도 이번에 처음으로 이렇게 시간을 넉넉하게 들여서 아이들에게 물은 듯 싶습니다. 교육과정을 전면적으로 들어 엎은 것이 마음의 여유를 조금 더 준 듯 합니다. 진도에 쫓기지 않고, 아이들과 충분히 배울 수 있는 시간을 만든 것. 어쨌든.

 

우리 교실에서 위 나눗셈을 할 줄 아는 학생은, 스스로 생각해 볼 시간은 갖지 못한 채 방법만 배워서 온 아이들일 것입니다. 학교 바깥에서는 아이들의 사고를 확인하지 않습니다. 그저 옳은 방법만 가르치고, 그 방법의 원리만 설명하고, 방법을 연습시킬 뿐.

 

미리 배워오지 않은 아이들에게 초점을 맞추어 하는 수업을 통하여, 아이들이 조절 과정 없이 그저 동화되기에만 바쁜 배움을 하고 있다는 것을 알게 되었습니다.

 

 

아이들은 왜 위와 같이 풀게 될까요?

 

위와 같이 푼다고 대답한 아이들에게 이유를 물었을 때, 아이들은 '덧셈/뺄셈을 그렇게 풀기 때문'이라고 답하였습니다.

 

아이들이 가지고 있는 연산 경험은 덧셈과 뺄셈, 곱셈의 경험입니다. 분수의 덧셈과 뺄셈 방식은 분모가 같은 경우 (분자)±(분자)를 계산하여 (계산된 분자)/(분모)의 꼴로 나타냅니다. 곱셈은 분자는 분자끼리, 분모는 분모끼리 곱하여 나타냅니다. 그런데, 분수의 곱셈을 풀 때의 아이들 모습을 가만 보면, 이를 덧셈과 뺄셈의 방식으로 푸는 아이들도 있습니다. 다만 간과하거나 미처 알아차리지 못한 채로 분수의 나눗셈까지 오게 됩니다.

 

우리는 수학을 가르치고 배울 때, 그저 방법만 가르쳐도 잘 푸는 아이들을 '수학을 잘 한다'고 생각하는 경향이 있습니다. 그렇지 않습니다. 방법만 가르쳐도 잘 푸는 아이들 모두가 끝까지 그렇게 잘 풀지 않음을 경험으로 알고 있습니다.

 

게다가 어떤 아이들은 방법만 가르치면 도무지 받아들이지 못하는 아이들이 있습니다. 분수의 나눗셈을 배우는 시기쯤 되면 이제 그런 아이들이 하나 둘 씩 교실에서 힘들어하는 모습을 보입니다.



어떻게 가르쳐야 할까요?

 

 

아이들에게 던졌던 반문은,



 

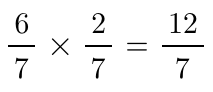
인가 였습니다. 나눗셈을 덧셈/뺄셈 풀듯이 그렇게 풀었다면, 곱셈도 그렇게 푸는가에 대한 반문이었습니다. 여기에서 일곱 명 중 너댓명이 위의 나눗셈과 같은 풀이는 문제가 있다는 생각을 한 듯 합니다.

 

여기에서 덧셈적 사고와 곱셈적 사고의 차이를 가르칠 수 있으면 좋을 듯 합니다.

 

덧셈적 사고는, 수직선 방식의 1차원적 사고입니다. 수직선 위에서 좌표가 앞뒤로 오고가는 방식으로 덧셈과 뺄셈을 소개할 수 있습니다.

 

그러나 곱셈적 사고는, 직사각형 넓이 방식의 2차원적 사고입니다. 곱셈 모델을 설명할 때 사용하는 가장 직관적인 모델은 직사각형 모델입니다. 바둑알 모델도 직사각형 모델의 변형에 가깝습니다.

 

아이들에게



 



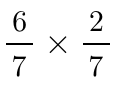
의 방식을 설명하기 위하여 세로로 7등분 한 단위 넓이의 직사각형 중 여섯 부분을 택한 것에서 다시 가로로 7등분 한 단위 넓이의 직사각형 중 두 부분을 택한 것의 넓이를 구하는 것을 확인합니다. 결국 단위 넓이는 49등분 되어 드러나게 되고, 이는 위 곱셈식의 값이 49분의 12가 나오는 원인이 되어 줍니다.

 

 

그러나 사실 나누는 수가 분수인 분수의 나눗셈은 이 모델로 명확하게 설명할 수 없습니다. 이는 나누는 수가 소수인 소수의 나눗셈이 나눗셈의 세로셈 알고리즘으로 풀리지 않기 때문에 나누는 수의 소수점을 옮겨서 자연수의 나눗셈으로 고쳐 푸는 것과 일맥상통한다고 볼 수 있습니다.

 

그래서 우리 교과서에서는 분수의 나눗셈도, 소수의 나눗셈도 공히 자연수의 나눗셈 모델을 사용하여 설명하는 방식을 취하고 있(었)습니다. 저는 이 방식이 좋다고 생각하고 있습니다.

 

비록 분수의 곱셈과 궤를 같이할 수 없지만, 자연수의 곱셈/나눗셈 모델과 함께 할 수 있는 모델이라서 아이들의 이해를 연계하여 도울 수 있다는 생각이 들기 때문입니다.

 

자꾸 새로운 모델을 시도할 필요가 없습니다. 왜냐하면, 어차피 분수의 나눗셈이나 소수의 나눗셈, 특히 제수가 자연수가 아닌 나눗셈의 경우에는 아이들 수준에서 만날 수 있는 가장 추상화된 방식이기 때문에 어차피 알고리즘으로 넘어갈 수 밖에 없습니다. 당장 중학교에만 가도 더 이상 연산 모델을 사용하지 않습니다. 초등학교 수준에서 알고리즘으로 해결할 수 있는 부분에 대해 억지로 모델을 구축하여 이를 통해 이해시키려고 하지 않았으면 좋겠습니다. 자연수의 나눗셈 방식으로 충분히 설명할 수 있습니다.

 

 

 



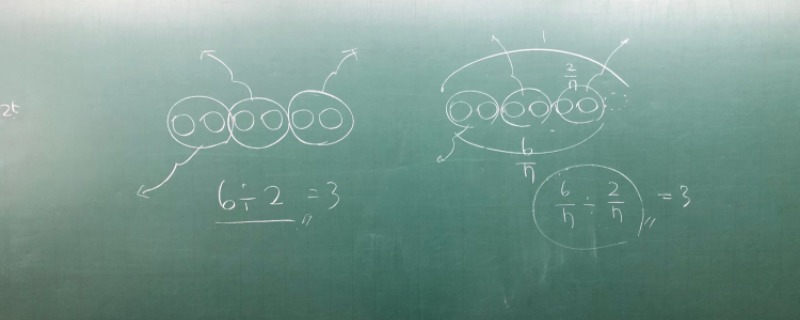
그런데 2015 개정 교과서는 이상한 모델을 하나 가지고 오고 있습니다.

 

가령,



3분의 2시간 동안 5분의 4 킬로미터를 갈 때, 한 시간 동안 몇 킬로미터를 가는가

 

라는 문제가 있다고 하죠. 이 문제를 우리 교과서는 아래와 같이 풀이하고 있습니다.

 

 

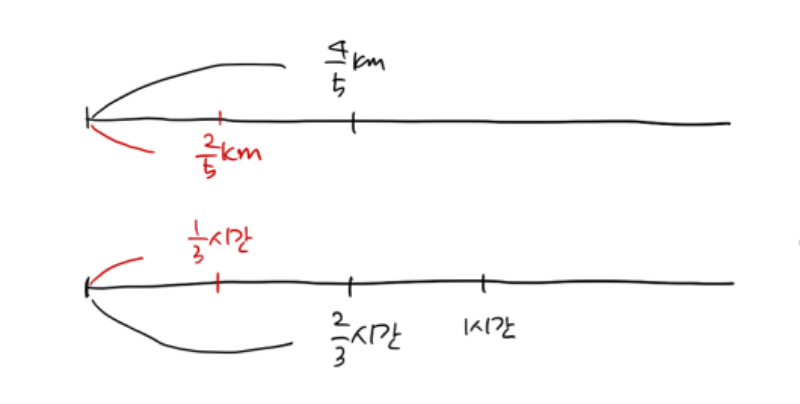
나누는 수(제수)를 역수로 고친 후, 나눗셈 기호를 곱셈 기호로 고치는 알고리즘을 설명하기 위한 것이라고 생각하지만, 엄밀하게 이는 비례식을 기반으로 한 설명입니다.

 



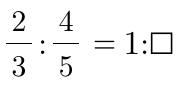
를 드러내는 이 방식의 문제는, 이 설명이 비례식을 배우는 4단원 이전에서 나온다는 점입니다. 물론 교과서를 집필한 분들이야, 그래서 단위 시간 - 한 시간 - 에 이동한 거리를 구하게 하는 등으로 비례식을 세워서 풀지 않아도 되도록 하였다고 말씀하시겠지만, 아마 학교에서도 학원에서도 비례식을 세워서 쉽게 쉽게 설명하는 식으로 아이들을 연습시킬 것입니다. 눈가리고 아웅이 되는 셈이죠. 정상적인 교육이 될 리가 없는데, 이런 식으로 교과서를 편제하면 과연 정상적인 학과 교육이 되는 건가요?

억지로 설명하여 아이들을 힘들게 하는 것보다, 그냥 쉽게 안내하는 편이 나을지도 모르겠습니다. 그러고보면 참 우리 교과서는 방향을 아이들 친화적으로 잡지 못하고 있습니다. 앞선 배움을 충분히 체화시키지도 못했는데 그저 다음 설명을 풀어 놓기 바쁘고, 그 설명도 과유불급인 셈이니 말입니다. 아이들의 이전 배움을 단단히 하고 그 위에 방법적인 부분을 올리는 것이 아이들이 조금 더 수학을 쉽게 생각할 수 있는 교수-학습이 되지 않을까 싶기도 합니다.

아니면, 아예 분수와 소수의 나눗셈 중에서 제수가 자연수가 아닌 부분은 중학교로 올리던지요. 아이들의 발달 단계를 고려하여 초등과 중등의 성취기준을 나눌 때, 추상화 된 방식으로 설명하는 것은 중학교로 올리고, 구체적인 방식으로 설명할 수 있는 것은 초등학교에서 가르치는 것으로 편제해도 나쁘지 않을 것이라고 생각합니다.

이미 할 수 있는 아이들에게도, 새로 배우는 아이들에게도, 왜 분수의 나눗셈 풀이 중 나누는 수(제수)가 분수인 나눗셈은 다른 나눗셈 풀이 방식과 다른지 자연수의 나눗셈 풀이 모델로 안내하였습니다. 그 기저에는 분수의 덧/뺄셈과 분수의 곱/나눗셈(중에서도 제수가 자연수인)의 접근 방식이 왜 다른지도 안내하였습니다.

이제 아이들은 이를 바탕으로 분수의 나눗셈 문제 상황이 어떤 것이 있는지 발표하고, 문제를 직접 만들어 보았으며, 이를 돌아가면서 풀이하여 보았습니다.

 

 

아에드 인 마이오렘 델 글로인