[2009개정 6학년 2학기 수학] 1. 쌓기나무
6학년 2학기 수학 1단원인 [쌓기나무]의 교과(용 도)서는 다음과 같은 학습목표를 가지고 있습니다.
1) 쌓기나무의 수를 구할 수 있어요 (1) 밑도안 이용하기
2) 쌓기나무의 수를 구할 수 있어요 (2) 층별 개수 세기, 묶어 세기 등
3) 위, 앞, 옆에서 본 모양을 그릴 수 있어요
4) 전체 모양을 알 수 있어요
5) 조건에 따라 모양을 만들 수 있어요
6) 여러 가지 모양을 만들 수 있어요
1단원과 관련된 성취기준을 토대로, 백워드 설계 1단계 과정, 배울 것 선정하기를 한 결과는 아래와 같습니다.

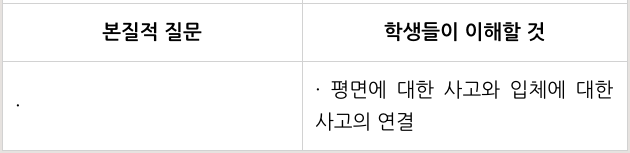
그런데, 1단원에서 '본질적 질문'을 도무지 선정할 수 없었습니다. 쌓기나무와 관련된 성취기준이 단원의 본질적 질문을 담아내고 있지 못하기 때문입니다. 쌓기나무는 이전과 이후의 어떤 단원과도 연계성을 갖지 못하는 단원입니다. 공간감각을 체험할 수 있는 단원이기 때문에 그저 블록들을 쌓아보기만해도 충분히 의미있는 교수-학습 과정이 될 수 있습니다. 그런데 공간감각이라는 것이 무언가 성취 결과로 드러날 수 있는 것이 아닙니다. 그렇다보니 공간감각을 통해 쌓기나무의 개수를 구하고 평면적 사고와 입체에 대한 사고가 서로 관계를 이룸을 성취기준으로 만들었지만, 진짜 그것을 통해서 학생들이 공간감각을 경험하였는가를 생각해보면 확신할 수 없습니다. 제가 '본질적 질문'에서 실패한 이유는, 그것을 하려면 생각의 비약이 이루어져야 한다고 생각했기 때문입니다.
그래서 1단원은 본질적 질문 없이, 성취기준을 바탕으로 한 배움이 일어날 수 있도록 진행하였습니다.
첫 시간은 쌓기나무를 주고 마음대로 쌓아보게 하는 시간을 가졌습니다. 목표도 없고, 과제도 없으며, 내심 바라는 바도 없는, 그저 쌓아보는 것.

배움의 목적이 공간감각이라면, 그저 이렇게도 저렇게도 쌓아보는 경험이 아이들에게 더 유의미할 수도 있을 것이라고 생각했습니다. 모둠별로 충분한 쌓기나무 블럭을 가지고 서로 즐겁게 쌓는 모습을 보면서, 요즘 아이들이 얼마나 목적 지향적인 활동의 홍수 가운데에서 지내는지 생각해 보게 되었습니다. 활동의 결과로 무언가 눈에 보이는 것을 배워야 하는 요즘 아이들. 그게 아이들을 즐겁게 만드는 배움인지 생각해 봅니다.
동기부여, 라는 말이 있죠. 아이들의 동기를 잔뜩 부여해놓고, 목적을 가진 활동으로 그 동기를 확 꺾어버리는 교수-학습 과정이 얼마나 많은지요. 동기부여만 40분 내내 해도, 아마 아이들에게 충분한 동기가 부여되었다면, 나머지는 아이들이 알아서 해 낼 수 있을 것입니다. 동기를 던질 수 있는 그런 교수-학습 과정을 진행하고 싶다는 생각이 새삼 들었습니다.

그리고 (어쩔 수 없이 선생이라서) 두 번째 시간에 학생들에게 준 해결 과제는,
앉은 자리에서 (일어서지 않고) 쌓여진 쌓기나무 입체를 보고 그 개수를 정확하게 알 수 있는 방법
알아보기였습니다. 우선 개인별로 학습지를 채워보도록 하였습니다.

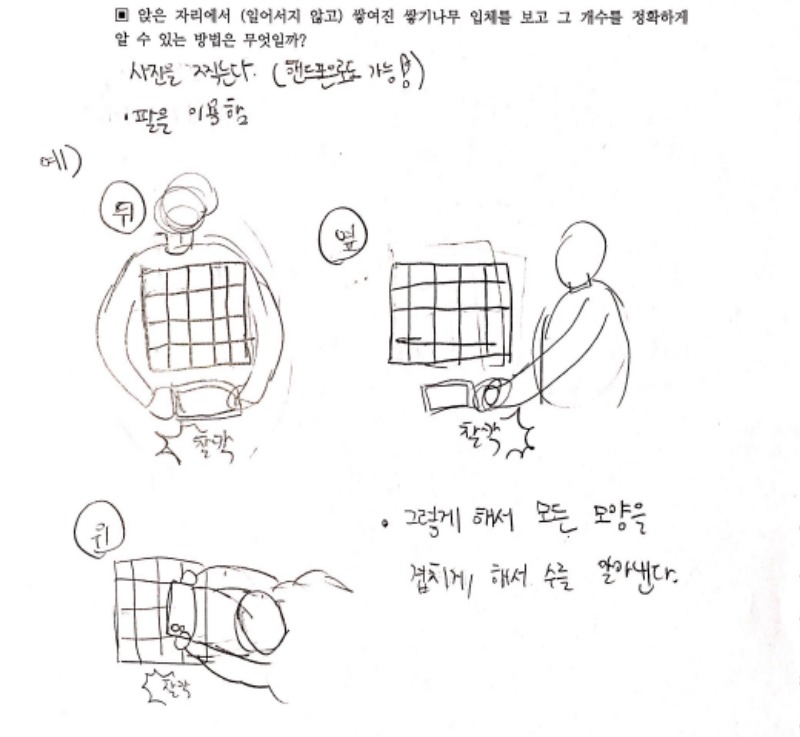
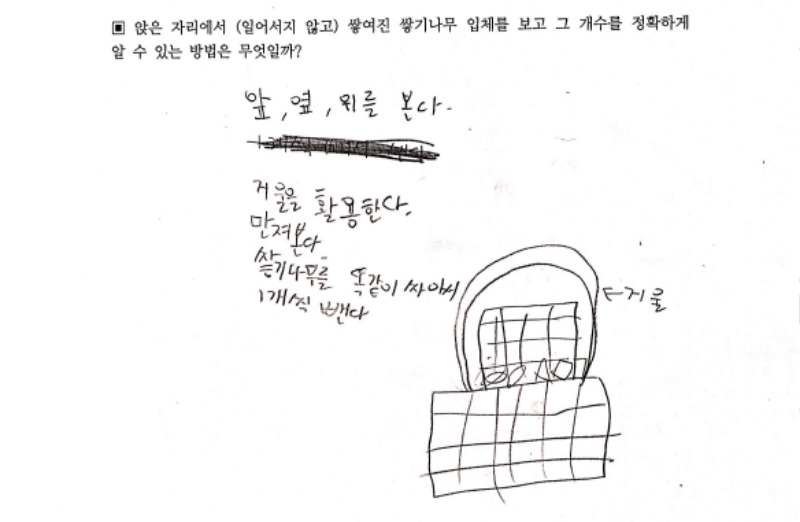

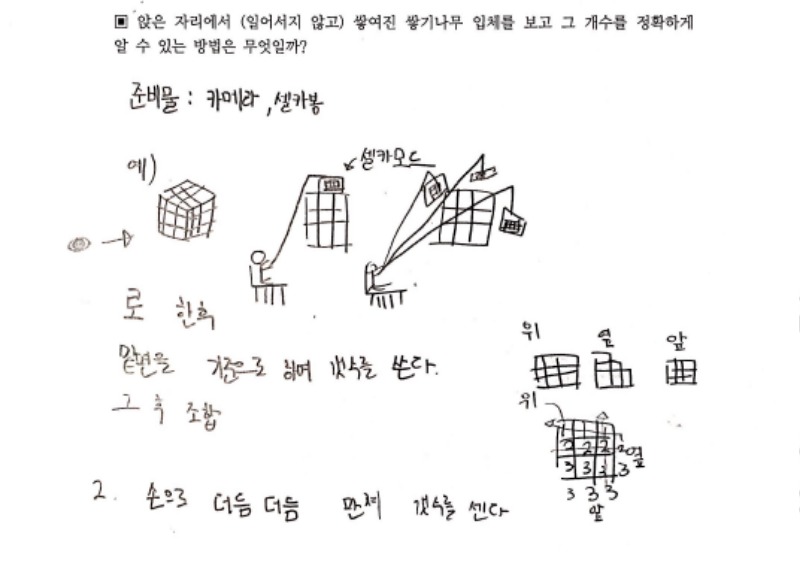
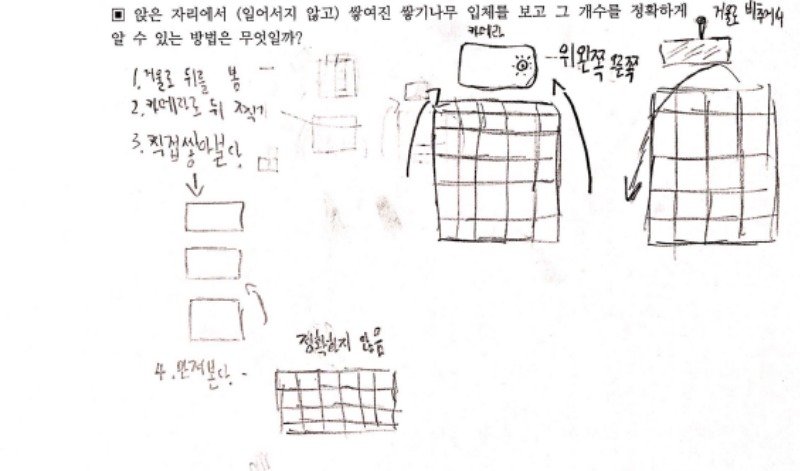


많은 학생들이 한 쪽만 보아서는 알 수 없고, 우선은 뒤를 봐야 더 잘 알 수 있겠고, 가능하면 위, 앞, 옆이라도 봐야 정확한 개수를 구할 수 있다는 답을 했습니다.
그리고 아이들 다운 답. 만져본다, 부순 다음 센다 등등등.
학습지를 가지고 모둠별로 가장 좋은 방법을 모아보도록 하였습니다.






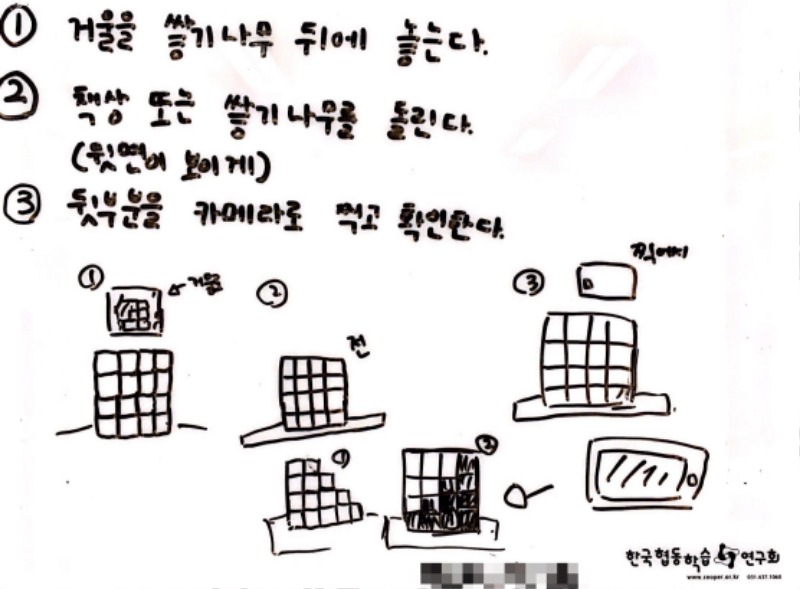

아이들 다운 답 - 도라에몽... - 을 제외하면, 대부분의 답은 보이는 앞면 말고 다른 면도 봐야 알 수 있다, 는 것이었습니다.
이렇게 본다면, 아이들은 입체도형의 형태는 평면의 모양을 통해 더 명확하게 알 수 있다는 생각을 하고 있는 것이고, 위 백워드 설계 1단계 표에서의 '학생들이 이해할 것'에 어느 수준 도달하였다고 볼 수 있는데, 수업 당시에는 그렇게 생각하지 못했습니다.
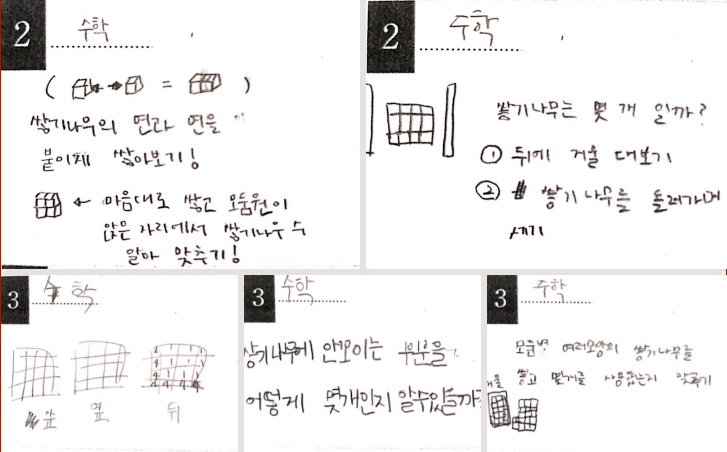
이 쯤에서 2016년 학생들의 모둠 활동 결과물.

재작년 아이들의 답은 교과(용 도)서에서 이야기하는 바와 유사합니다. 왜냐하면... 이런 답이 나올 수 밖에 없도록 교과(용 도)서를 펼쳐두고 수업을 했었기 때문입니다. 올해는 교과(용 도)서는 펴지 않고 그냥 교수-학습 과정을 진행하니까, 분명히 선행학습을 하였을 아이들도, 밑도안에 대한 이야기 없이, 위, 앞, 옆모양을 통해 알 수 있다는 조금 더 성취기준에 근접한 생각들을 바로 했습니다.
그런데, 교사가 아이들의 제출 답안 중에 교과(용 도)서의 답이 없으니 당황을 했던 듯 싶습니다. 아이들에게 다른 미션을 즉석에서 제시하였습니다.

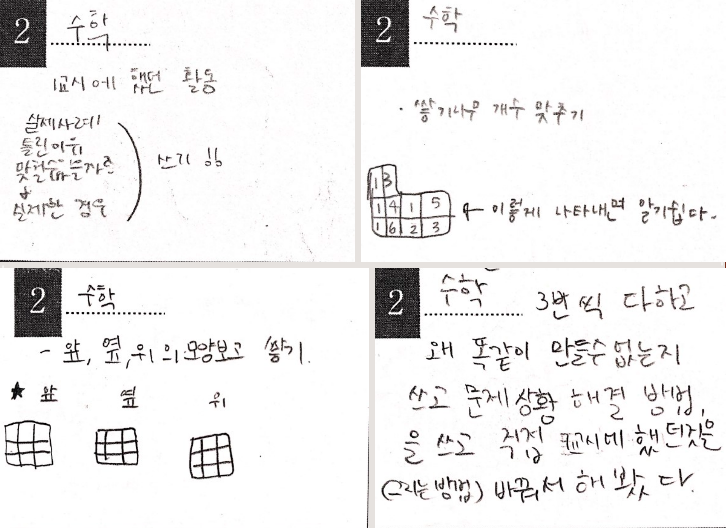
위와 옆에서 본 모양이 위와 같을 때, 이 개수를 명확하게 '표시'할 수 있는 방법이 무엇이겠느냐.

위에서 본 모양은 위와 같구요. 밑도안에 대한 언급을 하고 싶었을 것입니다. 결국 아이들에게 제시한 것은,

위와 같은 '방식'으로 쌓기나무의 개수를 명확하게 드러낼 수 있다. 이 수업이 끝나고 꽤나 후회를 했습니다. 그냥 학생들의 답안을 인정하고, 이런 방법을 제시하지 않고, 그냥 다음 과제로 나갔어야 하는데 말이죠. 오히려 이런 '방법'이 아이들의 자연스러운 사고 진행에 꼭 장애물이 된 듯 해서 꽤 큰 아쉬움을 오랫동안 가졌더랬습니다.
물론, 알려주면 좋죠. 그러나 위의 '방식'이 앞으로 배울 수학 도형 영역에서 하등 중요한 것이 아니라면, 차라리 섣부른 교사의 개입보다는, 학생들의 다채로운 생각을 이야기 나누면서 학생 스스로 정리할 수 있는 시간을 주는게 낫지 않았을까 싶습니다.
아래는 수업 후 학생들의 배움일지.



세 번째 시간과 네 번째 시간은, 모둠별로 퀴즈를 해결하는 시간을 가졌습니다. 네 명 모둠에서 우선, 한 어린이가 다른 친구들 보지 않도록 쌓기나무를 쌓습니다. 왼쪽에 있는 어린이만 쌓은 쌓기나무를 보고 위, 앞, 옆에서 본 모양을 그립니다. 그렇게 그린 모양을 그 왼쪽 어린이만 보고 쌓기나무를 쌓습니다. 그리고 마지막 어린이는 그렇게 쌓은 쌓기나무를 보고 쌓기나무의 위, 앞, 옆에서 본 모양을 그립니다. 그리고 서로 비교.
보드게임 중 텔레스트레이션의 방법을 응용해 보았는데... 아래는 활동 모습.



아주... 난리가 났네요. (쿨럭) 아이들을 너무 얕잡아본(!) 덕입니다. 당연히 교과(용 도)서의 예시처럼 간단하게 쌓아갈 줄 알았는데, 아주아주 복잡다단하게 쌓아 버렸습니다. 아이들은 이 복잡한 입체도형을 평면으로 완벽하게 표현해 낼 수 없다는 것을 알아버렸습니다. 초등 수학 교육과정에서는 보이는 평면만으로도 입체로 옮길 수 있어야하는데, 아이들은 너무 일찍 성숙(!)해 버린 셈이죠. 이런 결과까지 생각하지 못한 교사의 문제입니다.
그러나 한 편으로는 비록 성취기준에 맞는 활동이 되진 못하였지만, 오히려 학생들이 이 과정을 통해 도형의 평면과 입체 사이에 존재하는 위상에 대해서 생각할 기회가 되지 않았을까라는 생각을 해 봅니다. 이 지점에서, 배움을 조금 더 명확하게 가다듬을 수 있는 지점을 생각해 볼 필요가 있지 않나 생각하게 됩니다. 과제는 교사의 몫이니, 고민해 보겠습니다.
이 활동 이후에, 학생들은 입체를 평면으로 표현하였을 때 평면이 다시 입체로 표현되지 않는 상황에 대해 모둠별로 토의하고 이에 대해 기록하여 발표하였습니다.

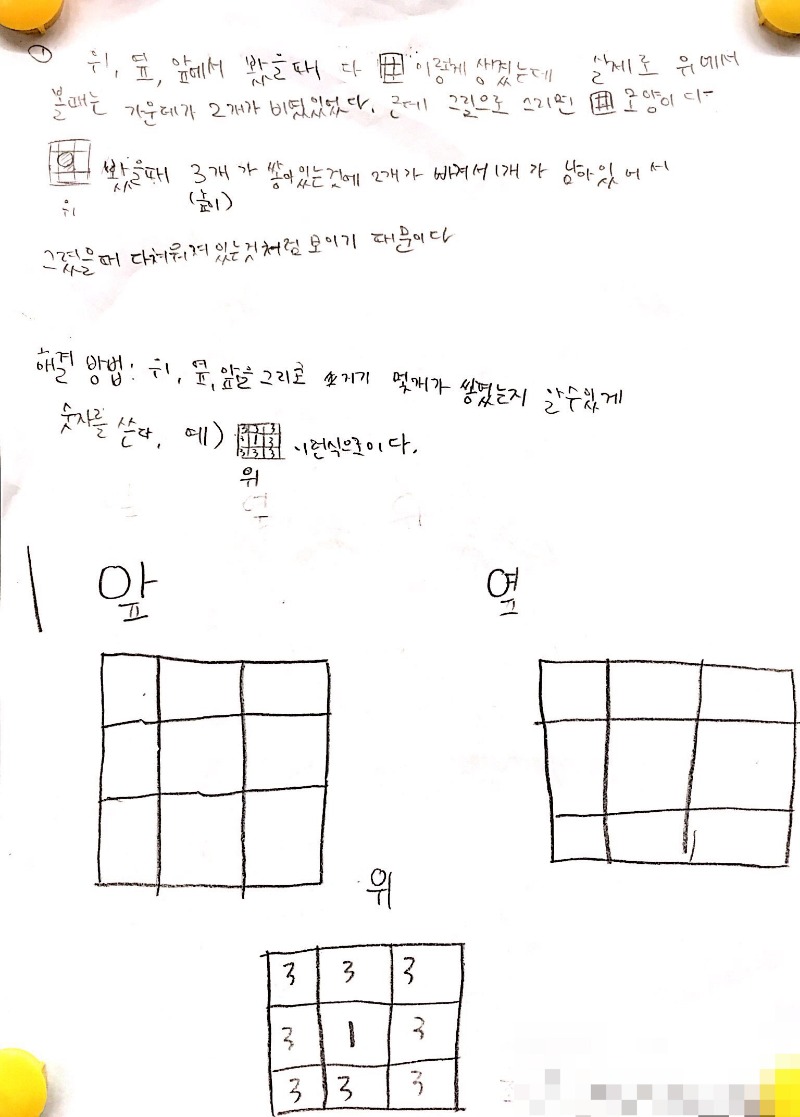


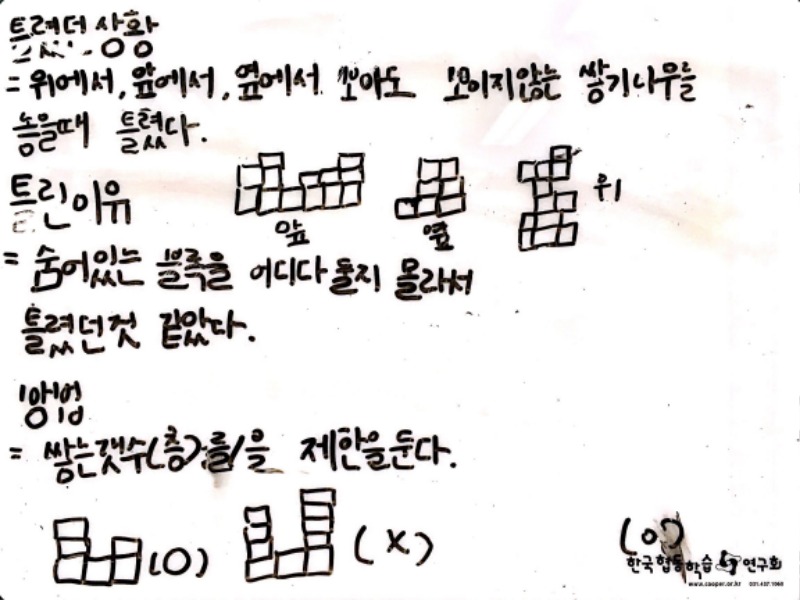
어떤 어린이들은 쌓기나무를 너무 어렵게 쌓았다거나 혹은 그림이 틀렸다거나 하는 이유를 제시하였는데, 몇 모둠은 속을 비우고 쌓았을 때 평면과 입체가 서로 일대일로 연결되지 않는다고 표현하였습니다. 그에 대한 해답으로는 개수를 알려주어 평면과 입체가 연결되는 가짓수를 줄이는 방법을 제안하였고, 한 모둠에서는 앞선 교수-학습 과정에서 이야기하였던, 위에서 본 모습의 단위 면적에 층 수를 표시하는 방식을 제안하였습니다. 이러한 문제 상황의 이해와 해결 방법의 제안을 통해 몇 모둠에서는 성취기준 상의 일정 수준에 도달했음을 확인하였습니다.
아래는 학생들의 배움일지 내용.


다섯 번째 시간부터 일곱 번째 시간은, 연결큐브를 가지고 교수-학습 과정을 진행하였습니다.
우선, 연결큐브로 자유롭게 이런저런 모양을 만들어보는 활동부터 하였습니다.

계속 아이들이 단위부피로 무언가를 만져보고 꾸며보는 자유시간을 주고 있습니다. 그러면서 크게 어렵게 여기지 않을 과제들을 함께 해결하고 있습니다.
자유시간을 가지던 중에 과제를 투입하였습니다. 과제는,
연결큐브 네 개로 만들 수 있는 입체도형은 몇 개인가?
1) 겹치는 것이 없으며
2) 빠진 것이 없다는 것이
분명하게 드러나도록 그 방법과 함께 구하시오.
연결큐브를 사용하여 재미나게 만들던 아이들이, 이제 과제를 호기심있게 받아들입니다.


돌리고 뒤집고 움직여서 같은 것은 같은 것으로 처리. 거의 모든 아이들이 모양을 일일이 만들어 볼 수 있는데까지 만들어 본 후, 자신들의 답을 구하였습니다.
그러나 진짜 과제는 지금부터입니다. 모두 같은 경험을 하였기 때문에, 이를 토대로 과제의 수준을 높였습니다. 앞선 과제에서 '연결큐브 네 개'를 '연결큐브 다섯 개'로 바꾸었습니다. 그리고 과제는 모둠 과제.
아이들의 집중력이 꽤나 높았습니다. 사실 2016년도에도 비슷한 활동을 했을 때 아이들이 굉장히 어려워했었고, 모둠 해결 방안도 도출되지 못했었는데, 아마도
1) 쌓기나무 블록과 연결큐브를 자유롭게 다룰 수 있는 충분한 시간이 학생들의 활동 참여에 긍정적인 영향을 끼쳤을 것
2) 구조화 된 과제 학습지의 사용과 이를 통한 명확한 자신만의 해결 방안 작성이 이후 과제에 대해 적극적인 자세를 가지게 했을 것
으로 생각하고 있습니다. 이런 교수-학습 과정을 또 진행할 기회가 있다면 같은 방식으로 한 번 쯤 더 해 볼 생각입니다.
아래는 학생들의 모둠 해결 방안 도출.
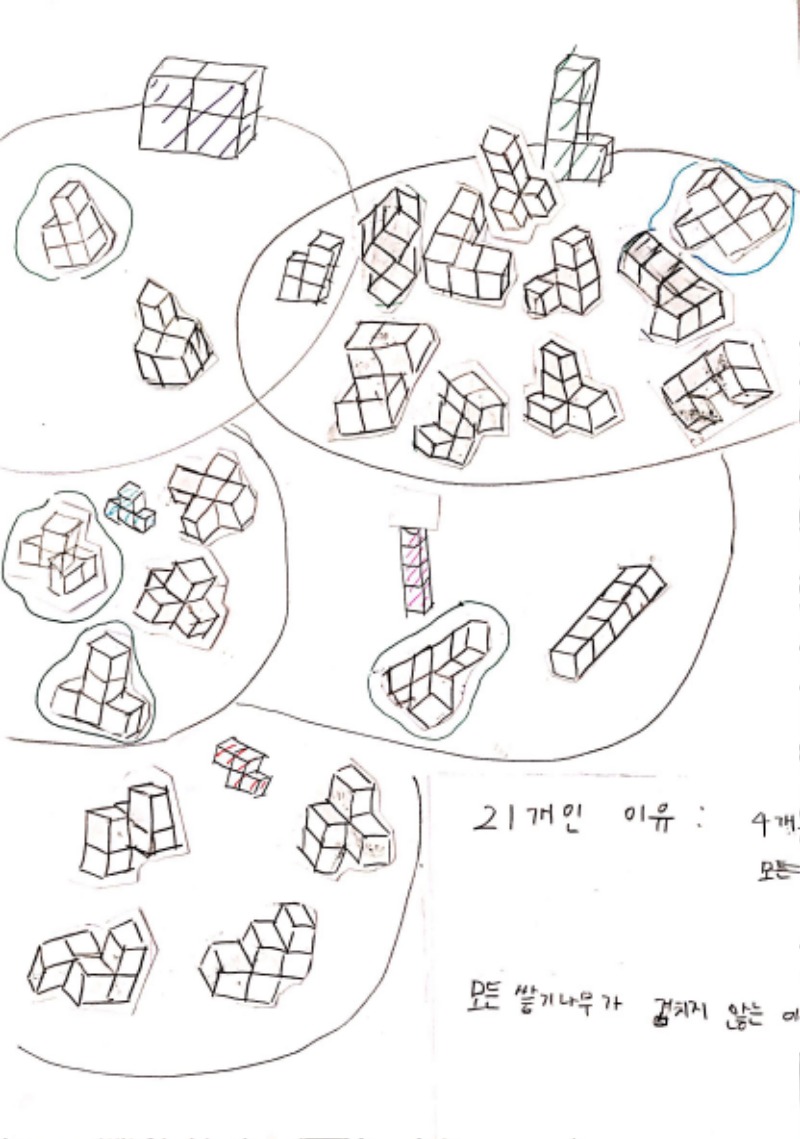
물론 정답에 이르지는 못하였지만, 위 모둠이 분류를 위한 기준 설정을 가장 잘 드러낸 모둠 해결 결과를 도출하였습니다. 결국 이런 기준 설정을 통한 분류가 경우의 수를 사고하는 기틀이 되어 줄 것입니다.
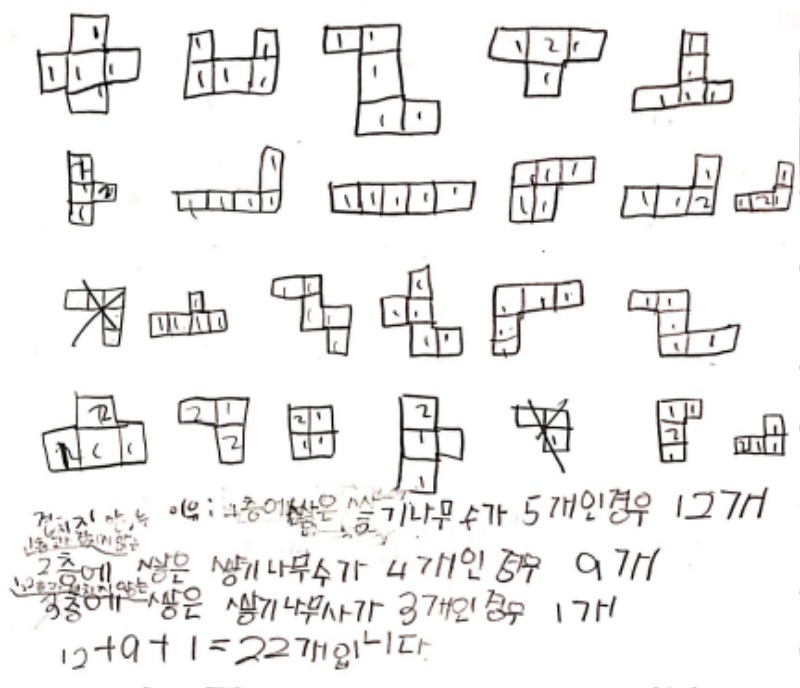
위 모둠도 높이의 위상 변화를 기준으로 분류의 방법을 사용하였습니다.

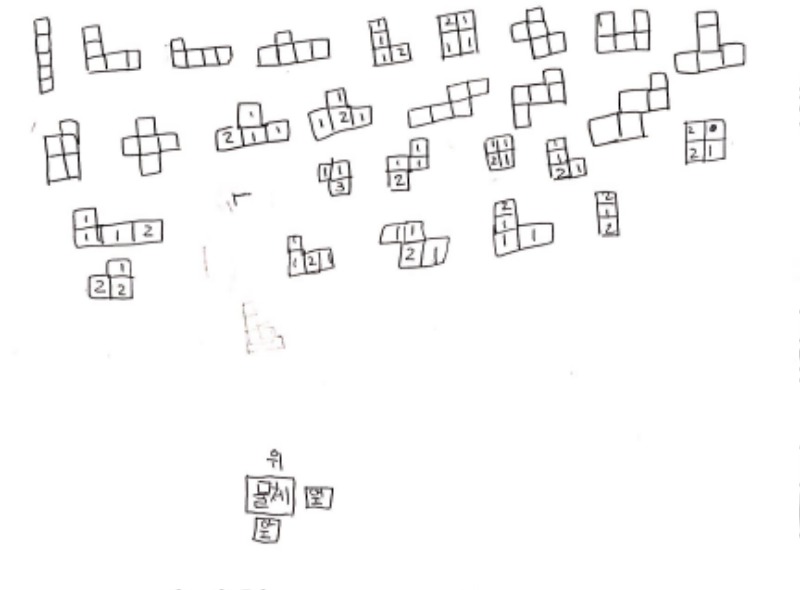
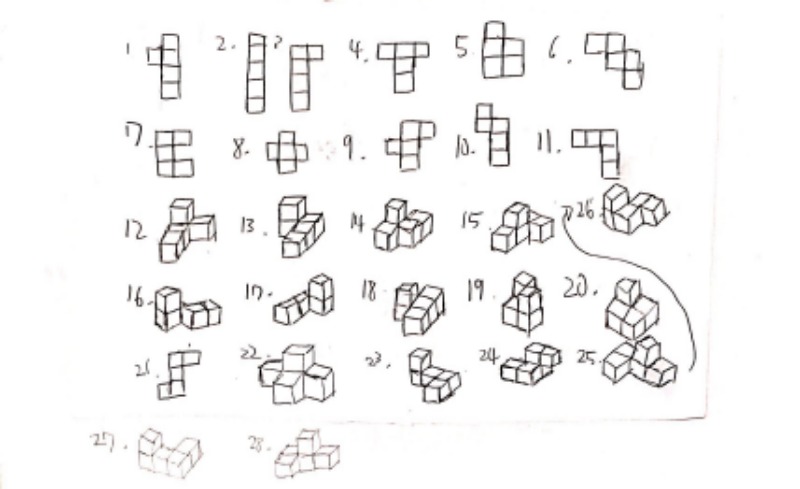

나머지 모둠은 '일일이 만들어 헤아려본다'의 수준을 넘지 못하였습니다. 그러나, 나름대로 앞서 배운 것을 토대로 평면 위에 입체를 표현하려는 다양한 시도를 드러내었습니다.

두 모둠이 합심하여 만든, 자신들의 연결큐브를 모두 털어 만든 서로 다른 경우들입니다.
아래는 담임 교사의 방법. 교사가 블록을 그리지 않고 간단하게 점을 찍고 수를 사용하는 것에 아이들은 적잖아 충격을 받은 모양이었습니다. 자신들은 왜 입체를 그리고 네모를 그리고 앉아 있었는지 모르겠다는, 세상 잃은 표정의 어린이들이 적잖게 보였습니다.

교사는 연결큐브 세 개, 네 개, 다섯 개로 순차적으로 늘어가는 것을 분류의 기준으로 삼는 것을 보여 주었습니다.
연결큐브 다섯 개로 만드는 서로 다른 입체도형의 개수를 구하는 것은, 실은 명확한 풀이 방법은 없습니다. 위의 방법에서 최선을 다해 겹치는 것을 골라내는 방법 밖에는 없습니다. 그러나, 아이들은 골라내는 과정에서 입체도형을 다각도로 생각하면서 공간감각을 자극해 볼 기회를 가졌습니다. 무엇보다 아이들이 어려워하거나 지루해보이지 않고 뿌듯해보이는 표정들로 수업을 마친 것이 좋았습니다.
마지막 여덟 번째 시간에는 교과(용 도)서의 '공부를 잘했는지 알아봅시다'를 풀면서 마무리하였습니다.
아에드 인 마이오렘 델 글로인

