[2009개정 6학년 1학기 수학] 2. 분수와 소수의 나눗셈 05-06 (2)
KimTeacHer
2
2674
0
2018.05.23 22:26
2. 분수와 소수의 나눗셈
05 분수의 나눗셈 계산원리 - 나누는 수 역수로 만들어 곱하기
두 시간 연차시 수업으로 두 가지 분수의 나눗셈 계산원리를 모두 이해해 보았습니다. 여담이지만, 올해 아이들과 면담을 진행하는 과정에서 몇몇 아이들에게 '올해의 수학 수업이 어떠한가'라는 질문을 해보고 있는데, 이번 주의 아이 하나가, 개념과 이론을 먼저 쭈욱 정리한 후에 교과서를 푸는 것이 자기에게 잘 맞는 듯 하다는 이야기를 해 주었습니다. 교과(용 도)서의 차시 구성이, 학생의 이해 절차를 분절하여 제시하고 있다면, 제가 준비하는 수업은 전체적인 흐름을 먼저 보여주는 교수-학습 과정으로 운영되고 있다는 차이가 있지 않나라는 생각이 들었습니다.
앞서, 분수의 나눗셈의 문제를 분모를 같게 만든 후 (분자)÷(분자)로 바꾸어풀게 되는 원리, 다양한 경우에서의 적용을 확인한 후 바로, 선행학습을 한 아이들이라면 이미 다 알고 있을 풀이인, 나누는 수를 역수로 바꾸고 나누기를 곱하기로 바꾸어 푸는 풀이 방법을 안내하여 주었습니다.
우선 교과(용 도)서는 원리를 이와 같이 설명하고 있습니다.
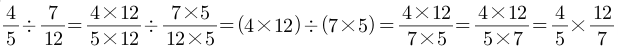
그래서 저도 재작년까지는 이것을 가르쳐주고, 이것을 평가에 출제하기도 하였는데... 생각해보면 초등학교 6학년 학생이 굳이 이 과정을 익힐 필요가 있을지 잘 모르겠다는 의문이 들었습니다. 솔직히 말하면, 교사인 저도 이 과정을 기억하는데 어려움을 겪는데 말이죠... 물론 교과(용 도)서 편찬자의 고충을 이해는 합니다. 아이들에게 무작정 '이렇게 푸는 것이다!'라고 말하고 싶지 않았을 것입니다. 그래서 저 위의 무리한 과정을 넣은 듯 한데... 그럴 것 같으면 아예 과정을 빼서 중학교로 올려보내는 것이 나을 수도 있습니다.
개인적인 생각에, 우리나라 아이들이 수학을 싫어하게 만드는 요인은 바로 위와 같이, 아이들의 발달 수준에 맞지 않는 과정들이 있기 때문이라고 생각하고 있으며, 교직에 처음 접어들때와는 달리, 지금에 와서는 교육과정의 수준이 지금보다 더 쉬워져야 한다는 믿음을 가지고 있습니다.
그래서, 요즘 대학생들의 수학 학습 수준이 너무 떨어진다고 한탄하는 대학 교수님들의 인터뷰를 보면 의아함을 가지고 있습니다. 대학에서 꼭 알아야한다고 생각하는 과정이라면, 대학에서 처음부터 차곡차곡 가르치면 됩니다. 우리나라 수학과 교육과정의 목표가 학생 일상에서의 수학화라면, 굳이 미적분을 배워가면서 수학화에 도달할 필요는 없습니다. 하위 과정으로도, 이차함수 정도로도 충분히 학생들의 수학화는 가능하다고 생각합니다. 미적분을 배우고, 공간에 대한 이해를 확장시켜가는 것은 대학에 가서도 충분히 할 수 있습니다. 대학이 완성형 인재를 뽑으려하기 보다는 가능성에 포커스를 맞추는 것이 필요하다고 생각하고 있으며, 그러기 위해 학생의 가능성을 다각도로 측정할 수 있는 신뢰할만한 지표를 개발하는 일을 부지런히 해나가야 할 것입니다. 그것이 어마어마어마한 등록금을 받아가면서도, 질적으로 훌륭한 배움에 대한 의문 부호를 남기는 대학 교육이 꼭 이루어야 할 부분이라고 생각하고 있습니다. 어쨌든.
올해 아이들에게는 위 풀이를 통해 '÷(분수)'를 '×(분수의 역수)'로 바뀐다는 것을 보여주기만 하였고 이를 굳이 학습할 필요는 없다고 이야기 하였습니다. 다만, 모든 알고리즘이 수학적으로 명확하게 정리된 과정을 가진다는것만 다시 한 번 강조하였습니다. 거저 나오는 알고리즘은, 없죠.
그 후에, 앞서 (분자)÷(분자)로 풀어보았던 모든 분수 나눗셈 문제를 다시 '×(분수의 역수)'로 고쳐서 풀어 보았습니다. 그 과정을 정리한 것이 아래 장면입니다.
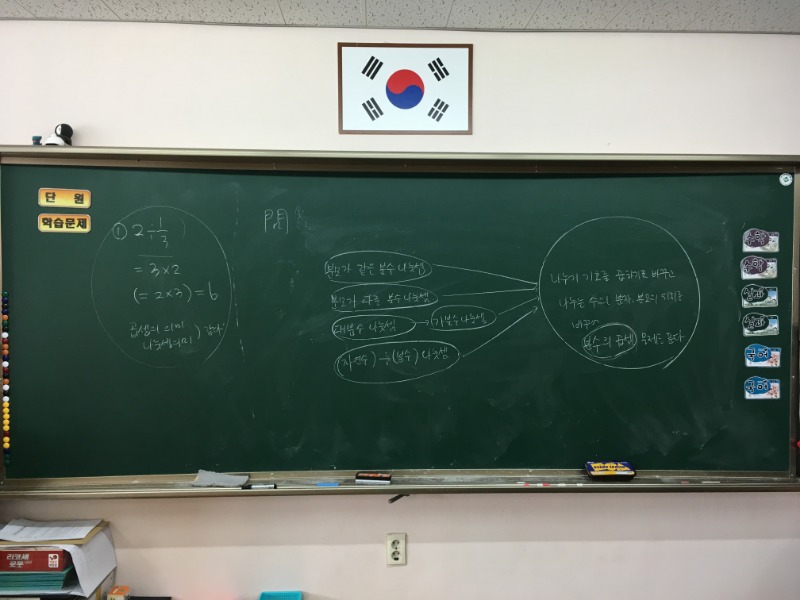
결국 앞서 '(분자)÷(분자)'로 바꾸어 풀 때보다 훨씬 간단한 풀이를 할 수 있게 되었습니다. 이를 정리해보면,
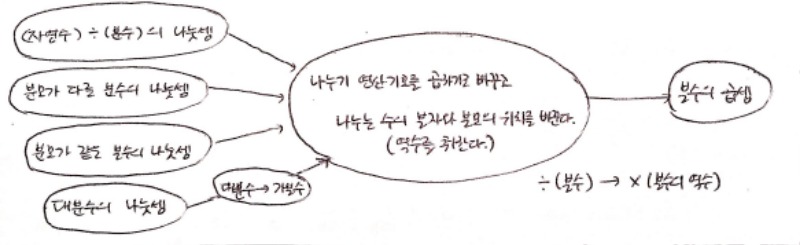
위와 같을 것입니다.
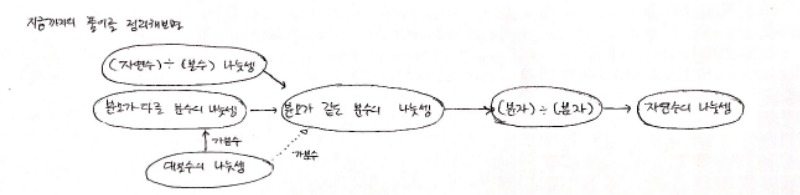
지난 시간에 다루었던 위 알고리즘보다는 확연히 간단하죠. 그래서 아이들에게 '×(분수의 역수)'로 바꾸는 방법을 택한다고 말해 주었습니다.
그렇다면 의문이 듭니다. 왜 굳이 분수 나눗셈 풀이를 '(분자)÷(분자)'로 푸는 것인가. 몇 가지가 있겠지만, 우선은 '(분자)÷(분자)'로 푸는 것이 알고리즘 사고 과정을 보여주기 때문이라고 설명하고 싶습니다. 아이들이 문제를 풀어가면서 나름대로 답에 이르는 과정을 위와 같이 구성할 수 있다면, 분수의 나눗셈 문제 하나를 푸는 것보다 더 나은 배움에 도달한 것이라고 할 수 있을 것입니다. 결국 수학은 일련의 알고리즘에 기반한 사고가 연속적으로 이루어지는 학문이라고 할 수 있을테니까요.
아래는 아이들의 배움일지 내용.


이제 여섯 시간에 걸쳐 분수의 나눗셈에서 배울 내용을 전반적으로 다 배웠으므로, 교과(용 도)서의 문제를 풀어보고 내용을 정리하기로 하였습니다.
아에드 인 마이오렘 델 글로인


