[6학년 수학] 2. 나눗셈 - 구체에서 추상으로

6학년 수학 첫 단원은 분수의 나눗셈 단원입니다. 한 단원 건너뛴 후 세 번째 단원에서는 소수의 나눗셈 단원을 맞이하게 됩니다. 분수의 나눗셈과 소수의 나눗셈을 나눈 이유는 무엇일까. 알고리즘 접근 방법의 차이 때문이라고 생각합니다. 분수의 나눗셈은 곱하기 분수의 역수 방법으로 풀이를 진행하고, 소수의 나눗셈은 전통적인 나눗셈의 세로셈 알고리즘을 사용하여 풀이하니 단원이 나누어 질 수 밖에 없습니다.

그러나 본질은 나눗셈입니다. 굳이 이를 분리할 필요를 느끼지 못하여, 저는 작년에도, 그리고 올해도 나눗셈이라는 큰 범주를 함께 아이들과 이야기 나눈 후, 분수와 소수의 개별적인 풀이 방법으로 접근하려고 합니다.

따지고보면, 분수의 나눗셈이든 소수의 나눗셈이든, 결국은 이전 학년에서 배웠던 방법으로 돌아가 문제를 해결하게 됩니다. 거기까지 가기 위해 새롭게 배우는 것은 사실 부수적인 것입니다.

그래서 저희 학급 수학 시간의 첫 진도는

나눗셈이란 무엇인가?

라는 질문으로 시작하게 되었습니다.

아브라함 발드의 이야기가 조금 일찍 끝나서, 첫 시간의 마무리에 위 질문을 던졌습니다. 두 명의 아이들이 답해주었고, 그에 대해 이야기 나누다가 시간을 마무리 하였습니다.

 

 

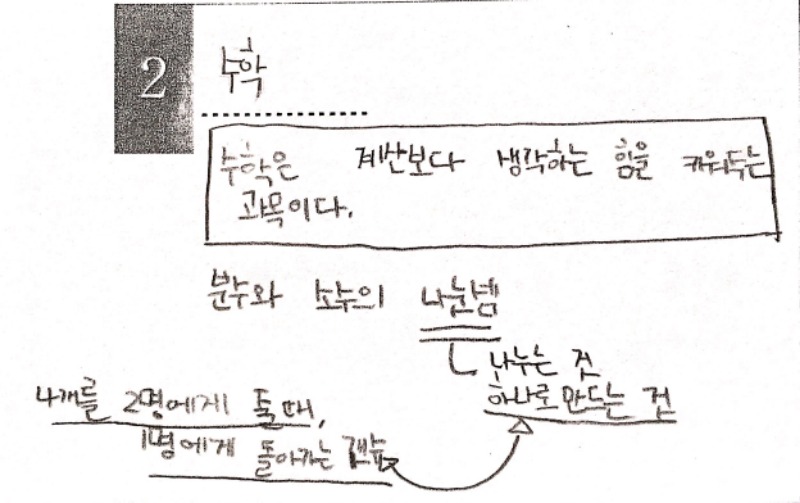
아이들의 답은,

 

나누는 것

하나로 만드는 것

이 있었습니다. '하나로 만드는 것'의 의미를 물었을 때, 아이가 대답한 답변은 '4개를 2명에게 줄 때, 1명에게 돌아가는 갯수'였습니다.

그 다음 시간에, 이 부분부터 다시 시작하였을 때, 아이들은 조금 더 다채롭게 답을 제시하였습니다.

 

 

두 명의 아이가 얘기한 것은,

 

어떤 수를 어떤 수로 나누었을 때, 최대한 나누는 것

몫과 나머지를 구하는 과정

이었습니다. 아이들의 답은 대체적으로 나눗셈의 의미에 대한 답보다는 절차에 대한 답에 가까움을 알 수 있습니다. 실제로 아이들의 나눗셈 배움은 절차에 치우친 것이었을 가능성이 커보입니다.

담임 교사가 제시한 키워드는 '몫'입니다. 우리가 나누는 이유는, 개인에게 돌아가는 '몫'을 명확하게 하기 위해서입니다. 그런데 우리 나눗셈은 한 가지 더 중요한 조건이 필요합니다. 모든 몫은 '똑같이' 나누어야 합니다.

만원을 3천원과 7천원으로 나누는 것은, 우리 나눗셈의 나눔은 아닙니다. 만원을 두 사람에게 나눌 때 5천원씩 똑같이 나누는 것이 우리 나눗셈 방법이고, 이 때 우리는 (만원)÷2 와 같이 식을 구성할 수 있습니다.

그래서 나눗셈이 똑같이 몫을 나누는 것임을 알았다면, 이제 나눗셈을 기호로 표시할 수 있다는 것을 알아야 합니다.

 

여섯 개의 귤이 있을 때, 두 명에게 나누어 주면 한 사람 당 몇 개의 귤을 가지는가?

 

6÷2=3

아이들은 위의 상황을 아래의 기호를 사용한 식으로 바꾸게 됩니다. 구체에서 추상으로 나아가게 됩니다.

그런데 생각보다 꽤 많은 아이들이 구체에서 추상으로 나아가는, 상황이 기호로 표시되는 이러한 과정에 익숙해보이지 않습니다.

물론 매 상황마다 하나하나 일일이 추상화되는 과정을 계속 보여줄 수는 없습니다. 그러나, 수학을 배우는 현장에서는 너무 빠르게 상황을 기호로 넘겨버리고 있습니다. 나눗셈 식을 푸는 방법은 과도하게 학습하는데, 나눗셈 식 상황을 이해하는 경험은 상대적으로 부족한.

그래서 상황을 몇 가지 더 이야기해 보기로 합니다.

선생님이 사탕 스무 개를 다섯 명에게 주면 한 사람에 몇 개 씩 갖게 되니?

카라멜 열 여덟 개를 세 개씩 나누어주면 몇 명에게 주게 되니?

등등등

사실 나눗셈은 똑같이 몫을 나누는 것이기도 하지만, 몫으로 똑같게 나누는 것이기도 합니다. 나누어 몫을 구할 수도 있고, 몫으로 나누어 구할 수도 있는. 위 두 번째 상황이, 학생들에게 돌아갈 몫이 세 개 씩으로 정해져 있는 상황에서 몫으로 나누는 상황이라고 할 수 있지요.

 

어쨌든 학생들은 이런 상황에서 익숙하게 답에 도달할 수 있습니다. 이런 상황에 대해 학생들은 이미 능숙하게 사고할 수 있을 만큼의 발달에 도달하였다고 할 수 있습니다. 굳이 기호로 바꾸지 않아도, 학생들은 쉽게 답을 구합니다.

그런데, 아이들의 사고를 들여다보면, 나눗셈 사고가 아닌 경우도 만날 수 있습니다. 위 카라멜 상황에서 학생들은,

18÷3

과 같이 생각하기도 하지만,

3×6=18

이기 때문에 답이 6이라고 말하기도 합니다. 상황은 나눗셈 상황인데, 방법은 곱셈을 사용하는. 작년에 이에 대해 두드린 바 있습니다.

 

 

사탕 스물 두 개를 네 명에게 주면 한 사람에 몇 개 씩?

나머지가 생기면, 아이들은 곱셈 사고로 나눗셈 문제를 해결하기가 어렵습니다. 사실 엄밀하게 말하면 곱셈 사고라고 할 수도 없습니다. 저학년 때 열심히 외운 곱셈구구가 효과를 발휘하는 것인지도 모릅니다.

스물 두 개를 다섯 명에게 주면, '나머지'가 발생합니다. 나머지를 어떻게 처리할지를 고민하는 과정에서 다루는 수의 범주가 확장됩니다. 그냥 나머지 상태로 놔 둘 것이냐, 아니면 남은 것을 똑같은 수량만큼 몫으로 나누어 줄 것이냐.

이 쯤 오면 이제는 상황을 다루는 것보다는 수 자체를 가지고 다루는 것이 조금 더 편해 보입니다. 상황을 기호로 바꾸어 표현하였다면, 상황은 이제 희미해지고 수와 기호만 남아 학생들에게 추상적 사고를 요구하게 됩니다.

실제 수업.

 

질문

나눗셈이란 무엇인가?

학생들의 답 이후 교사의 답

나눗셈은 개개인에게 돌아갈 똑같은 몫을 구하는 것이다.

(또는 전체를 개개인의 몫으로 나눈 것이다)

문제상황

여섯 개의 귤을 두 사람에게 나누어주면 한 사람에게 돌아가는 귤의 수는?

사탕 스무 개를 다섯 명에게 주면 한 사람이 받는 사탕의 수는?

카라멜 열 여덟 개를 세 개 씩 나누어 주면 몇 사람이 카라멜을 받을까?

상황의 확장

카라멜 스물 두 개를 네 개 씩 나누어 주면 몇 사람이 카라멜을 받을까?

 

 

아에드 인 마이오렘 델 글로인

 

- 지난 이야기 -