[6학년 수학] 8. 나눗셈(07)-방법의 이해

 

 

 

개학 후 두 번째 시간에는, 6학년 1학기까지 배운 나눗셈을 범주화 해 보았습니다.

 

아이들이 배우는 나눗셈은 크게 세 가지로 나누어 살펴볼 수 있습니다.

 

     자연수의 나눗셈

     분수 나눗셈

     소수 나눗셈

 

아이들과 우선 자연수의 나눗셈에 대하여 이야기 나누었습니다.

 

"자연수 나눗셈의 예시는 뭐가 있을까?"

 

아이들의 답은 10÷2, 1÷2, 8÷4, 12÷3, 100÷50, 1000÷20 등과 같이 이어졌습니다. 그러다가 꼭 그런 아이들 하나 있잖습니까. 숫자 막 이야기하는 친구들 말이죠. 1942÷1587 같은. 바로 그 때, 곧바로 되물어봅니다.

 

"그거 어떻게 풀어?"

 

당연히 풀이를 염두에 두고 말한 것이 아니기 때문에, 아이는 말문이 막힙니다. 연이어 다른 아이들에게도 물어봅니다. 이거 어떻게 풀어야돼?

 

한 두 명 씩, 아이들은 자기가 알고 있는 풀이를 말하기 시작합니다. 다 들어본 후, 말해주죠. 이런 문제는 수학 시간에 풀라고 하지 않아. 의미가 없잖아?

 

수학은 곤란하게 만들기 위한 과목이 아니라, 생각하는 역량을 돕는 과목이자 학문이기 때문에 굳이 의미없는 상황을 만들 필요가 없습니다. 그런데 어떤 문제집, 어떤 교사들은 그저 아이들을 곤란하게 만들 뿐인 문제 상황을 주고는 이걸 해결해야 수학을 잘 하는 것이라고 착각하는 경우도 있어 보입니다. 저도 한 때 그런 평가가 좋은 평가인 줄 알고 아이들에게 제시하기도 하였구요.

말도 안되는 곤란한 상황을 초등학교 때부터 연습할 필요는 없습니다. 특히, 말도 안되는 수나 상황으로 아이들을 곤란하게 만들 필요는 더더욱 없어 보입니다. 우린 혹시 그걸 해결하는 것이 수학을 잘 하게 만드는 것이라는 착각을 하고 있는 것은 아닌가요? 수학적으로 생각해야 할 상황에서, 아이들이 수학적으로 생각할 수 있게 만드는 것이 초등학교 교실 수학 수업에서 이루어져야 할 부분입니다.

 

그래도 기왕 아이가 이야기 한 상황이니 수를 약간 바꿉니다. 1942÷3. 그런 다음 처음부터 아이들이 말했던 그 수들을 어떻게 해결할지 묻습니다. 이 때 아이들은 크게 두 가지 방법을 말합니다. 분수로 고치거나, 나눗셈의 세로셈 알고리즘으로 해결하거나.

 

10÷2는 5이고, 1÷2는 2분의 1이며, 8÷4는 4분의 8이니 2, 12÷3은 3분의 12이니 4, 100÷50은 50분의 100이니 2, 1000÷20은 50 같이. 그러다가 1942÷3 쯤 오면 세로셈 알고리즘을 꺼내어듭니다. 1학기 때 몇 시간에 걸쳐 연습해왔기 때문에 아이들은 풀이 과정을 잘 알아봅니다. 저 또한 서둘러서 풀지 않고 천천히 풉니다.

 

1942에서 일단 3을 백 번만 빼 내자. 그럼 1642가 남겠네? 같이. 어차피 평생 사용할 알고리즘이기 때문에 천천히 연습해도 됩니다. 이미 능숙한 아이들에게는 너무 지루하지 않게, 아직 알고리즘이 익숙치 않은 아이들에게는 너무 빠르지 않게, 알고리즘의 속도를 조절하면서 천천히 서둘러서 (응?) 풀어봅니다.

 

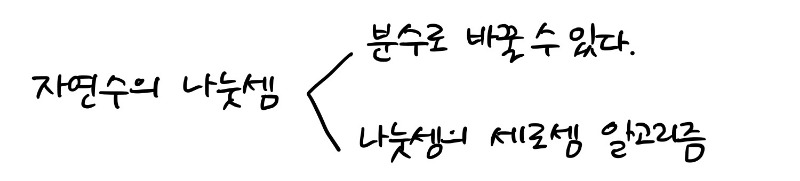
이렇게 자연수의 나눗셈을 살펴본 후, 분수의 나눗셈을 살펴봅니다.

 

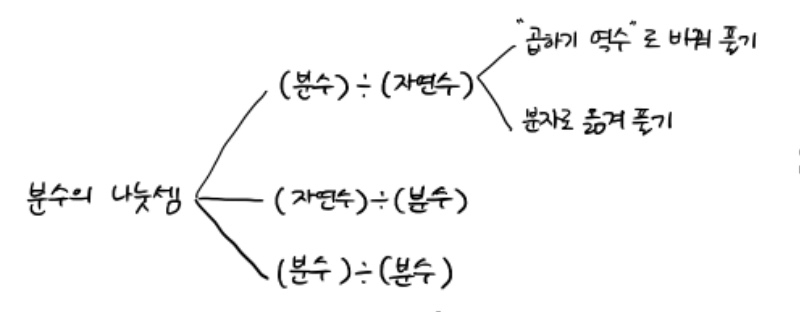
분수의 나눗셈은 크게,

     (분수)÷(자연수)

     (자연수)÷(분수)

     (분수)÷(분수)

상황이 있습니다. 이 중 (분수)÷(자연수) 상황은 6학년 1학기 때 배운 바 있습니다. 이를 토대로 2학기 때의 (자연수)÷(분수) 및 (분수)÷(분수) 상황을 살펴보고자 합니다.

 

문제를 하나 꺼내어 들었습니다.

 

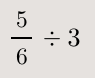
이건 어떻게 풀까?

 

아이들의 풀이는 단호합니다. 나누기를 곱하기로 바꾸고 1분의 3을 3분의 1로 바꾸어요. 이 때 물어봅니다. "왜 그렇게 풀지?"

 

1학기 교과서에서는 곱하기 자연수의 역수로 푸는 것을 직사각형 모델로 설명합니다. 아이들은 기억할 리 없습니다. 실은, 개인적인 생각에 그렇게 열심히 기억할 필요는 없다고 생각합니다.

 

우리 초등학교 교과서는 방법에 대한 이해에 너무 몰입하고 있습니다. 알고리즘의 복잡성이 있는 나눗셈의 세로셈 알고리즘, 혹은 곱셈의 세로셈 알고리즘 정도에서는 방법에 대한 이해에 조금 더 신경써도 좋겠지만, '곱하기 역수'로 풀이하는 것까지 그렇게 이해를 기반으로 한 방법의 소개에 매달리지 않아도 좋다고 생각합니다.

 

아래의 풀이는 2009 개정교육과정 교과용 도서에서, 분수의 나눗셈 방법을 설명하기 위해 제시했던 과정입니다.

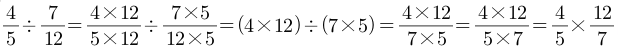
위 식은 분수의 나눗셈에서 '곱하기 역수'로 고쳐 푸는 알고리즘을 '이해'시키기 위해 교과용 도서가 꺼내어 든 방식입니다. 열심히 이해시키려고 노력하였지만, 결국 마지막에 남는 것은 등호의 왼쪽 끝 식과 오른쪽 끝 식 뿐. 이 두 식을 연결하는 중간 연결고리를 이렇게 복잡한 과정을 거쳐가면서까지 굳이 알아야 할까요? 굳이 이해시키거나 납득시켜야 할까요? 그럴 이유가 없습니다.

 

나눗셈의 본질은, 피제수에서 제수를 나누는 것이 본질입니다. 피제수가 자연수인가, 분수인가, 소수인가는 중요한 것이 아닙니다. 다만, 수가 속하는 범위에 따라 다른 방법을 취하곤 하지만, 분수의 나눗셈에서 취하는 '곱하기 역수' 방법에서 어려움을 겪는 아이들이 많지는 않으니, 그저 직사각형 모형 정도로 아이들에게 이렇게 된다고 알려준 후 이를 '이용'할 수 있도록만 해도 괜찮습니다.

 

오히려 나눗셈의 세로셈 알고리즘 같은 것을 초등학교 3학년, 이해하기도 어려운 그 시기에 알려주지 말고, 6학년 쯤해서 아이들이 알고리즘을 헤맬때 쯤 알려주는 방식으로 교과용 도서를 구성하는게 훨씬 나아보입니다.

이번 교육과정 개정과 함께 교과용 도서도 위 '곱하기 역수'의 이해법을 버리긴 하였습니다. 다만... 더 큰 문제가 있다고 생각하는 바, 그 까닭은 다음 글에서 두드려 보고자 합니다. 어쨌든.

 

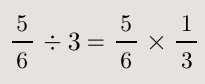
로 고치는 방법 말고, 6학년 1학기 교과용 도서에서는 다른 풀이도 하나 또 소개하고 있습니다.

 

 

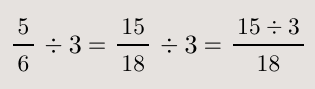
과 같이 푸는 방식입니다.

 

동학년 선생님과 이 방법에 대한 이야기를 잠시 나누었는데, 이 식을 관대하게 생각하시는 모습을 볼 수 있었습니다. 이 식 때문에 아이들이 2학기 분수의 나눗셈에서 (분자)÷(분자)로 문제를 해결함을 조금 더 직관적으로 이해하더라.

 

그 선생님의 말씀도 어느 정도 일리는 있다고 생각하였지만, 그럼에도 이 식은 문제가 있습니다.

 

1. 위 식으로 바꾸는 과정 자체가 번분수의 성질, 즉 분수의 바(bar) 위에 또 다른 분수를 두는 형태가 되어버린다는 점입니다. 번분수는 중학교 교육과정에서 다루죠. 저는 위와 같이 올리는 방식이 교육과정 상의 성취기준 범주를 넘어선다고 생각하고 있습니다.

 

2. 위 식과 같이 풀기 위해서 아이들로 하여금 분수의 분자와 자연수가 서로 나누어지는 수인지 아닌지 확인한 후, 나누어지는 수이면 자연수를 바로 분자로 올려서 풀게하고, 나누어지지 않는 수라면 나누어지는 수가 될 수 있도록 분수를 바꾸어 풀도록 하고 있습니다. 알고리즘은 풀이를 방법적으로 쉽게 접근하기 위해서 사용하는 것인데, 알고리즘을 사용하는 아이들에게 진입 장벽을 만들고 있습니다. 그리고, 6학년 아이들이 정말 힘들어하는 부분은, 분수와 소수의 나눗셈이 아니라, 약분과 통분 같은 5학년 때 다루었던 수학을 더 어려워한다는 것을 간과하고 있습니다.

 

3. 그리고 위의 알고리즘은 확장성이 없습니다. 이후에는 저런 방식으로 절대 문제를 풀지 않습니다. 6학년 2학기 분수의 나눗셈에서 소개하는 알고리즘은 (분자)÷(분자)의 풀이와 궤가 같다고 하더라도, 위 식이 훨씬 복잡합니다. 어렵구요. 굳이 위와 같은 식으로 연계점을 찾아 운영할 필요가 전혀 없어 보입니다.

 

개인적으로는, 굳이 위와 같이 '곱하기 역수'를 '이해'시킬 필요가 없었다고 생각합니다. 직사각형 모델 하나여도 족합니다. 모델로 이해하지 못하더라도, 방법적으로만 접근해도 괜찮다고 생각합니다.

 

6학년 1학기 때까지 배운, 분수의 나눗셈을 푸는 방식은 따라서 두 가지 방법으로 정리할 수 있습니다.

 

 

 

 

아에드 인 마이오렘 델 글로인