[WHY] 수학을 공부하는 2가지 이유
무슨 공부를 하길래 나라 잃은 표정을 하고 있니? 수학이구나. 수학은 그냥 곱셈, 나눗셈만 할 줄 알면 되는 거 아니냐고? 기특한 녀석. 선생님과 비슷한 생각을 했구나. 선생님도 덧셈, 뺄셈, 곱셈, 나눗셈만 할 줄 알면 되는 줄 알았어. 굳이 수학 공부를 따로 해야 하는지 궁금했지. 심지어 그 사칙연산도 계산기가 있잖아? 그 생각까지 들면 수학 공부의 의미를 더 찾을 수가 없겠더구나. 그저 중요 과목이라고 하니까, 대학 입시에 중요하다고 하니까 공부했었지.
그런데 수학은 입시를 위해서만 공부하기에 너무 아까운 학문이더구나. 수학을 공부하면 뭐가 좋냐고? 선생님은 두 가지를 이야기해 주고 싶다. 논리력과 창의력이다.
***
논리력은 개인적인 판단을 버리고 철저히 이성적으로 문제를 해결하는 힘을 말해. 문제를 파악하고, 식을 세우고, 답을 구하는 과정에서 수학자는 어떠한 가치 판단을 하지 않지. 그저 수학 규칙에 따라 움직여.
역사를 보자. 역사는 과거에 일어난 사실을 배우는 학문이야. 하지만 그 사실에는 사람의 판단이 들어가. 신라가 삼국을 통일한 사실을 두고, 민족의 통합에 기여했다는 판단과 외세의 힘을 빌려 이룬 반쪽짜리 통일이라는 판단이 존재하지. 심지어 신라가 삼국을 통일했다는 사실조차 의심받기도 해. 옛날 교과서는 통일 신라로만 가르쳤지만, 시간이 지나서는 발해를 포함한 남북극 시대라고 가르치지. 즉 역사 교과서는 사람에 따라, 시대에 따라 다르게 쓰일 수 있어. 국어와 영어 같은 언어도 시간이 흐르며 교과서가 변하기도 해. 과거 교과서에는 자장면이 맞다고 했지만 현재에는 짜장면도 맞는 것처럼. 당시 사람들의 언어 사용을 반영해서 새로운 문법이 필요하다고 판단한 거지. 도덕, 실과, 체육, 음악, 미술 모두 시대에 따라, 사람에 따라 교과서가 달라질 수 있어.
반면 수학은 그렇지 않지. 수학은 변하지 않는 정답을 구해야 해. 그 정답을 구하기 위해 필요한 것은 철저한 이성적 사고야. 1+2 = 3이라는 식에는 수학자의 논란이 없어. 시간이 지나도 변하지 않는 정답이지. 이런 학문은 수학이 유일해. 그런 점에서 아주 매력적이야. 수학을 공부하면 철저히 이성적으로 문제를 해결하는 힘을 기를 수 있단다.
***
창의력은 한 문제를 여러 가지 방법으로 풀 수 있는 능력을 말해. 1+ 2 + 3 + 4 + 5를 가지고 이야기해보자. 꽤 길어질 거니 각오하렴. 먼저 정답은 몇이지? 정답은 15, 단 하나지. 답은 논란의 여지가 없지만 풀이 방법은 하나가 아니야. 너는 어떻게 구했니?
첫째, 하나씩 더해서 구하는 방법이 있지.
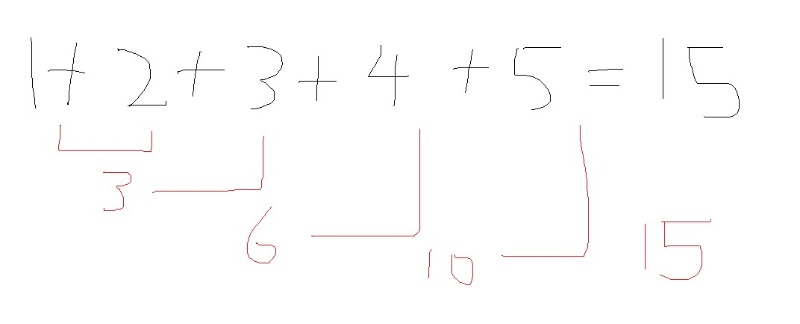
지극히 논리적이고 당연한 방법이야. 이 방법만 알면 되는 거 아니냐고?
그렇다면 다음 문제의 답을 구해 볼래?
1+2+3+4+ ... +99+100+101 =
물론 처음 방법처럼 차례대로 구할 수 있어. 하지만 계속 쓰다 보면 팔이 아프고, 짜증이 나고, 종이를 찢고 싶은 유혹이 들지. 그런데 간단히 구할 수 있는 다른 방법이 있다면?
다시 1+2+3+4+5로 돌아와보자. 처음 1과 끝의 5를 더하면 6이지? 두 번째 수 2와 끝에서 두 번째 수 4를 더해도 6이네. 그러면 다음과 같이 구할 수 있지 않을까?
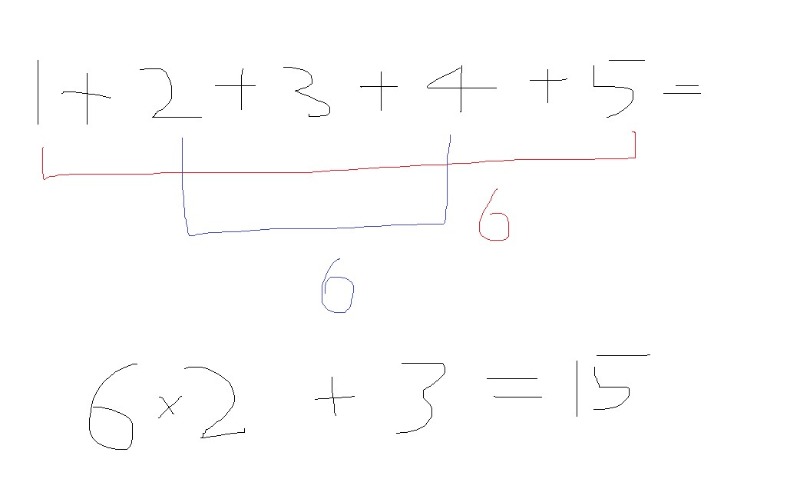
6이 두 번 있으니 곱하기 2로 구해주고, 가운데 3을 더해주면 되지.
무슨 생고생이냐고? 이 방법은 숫자가 커지면 힘을 발휘하지. 이 방법을 이용해서 1+2+3+4+ ... +99+100+101 =를 구해보자.
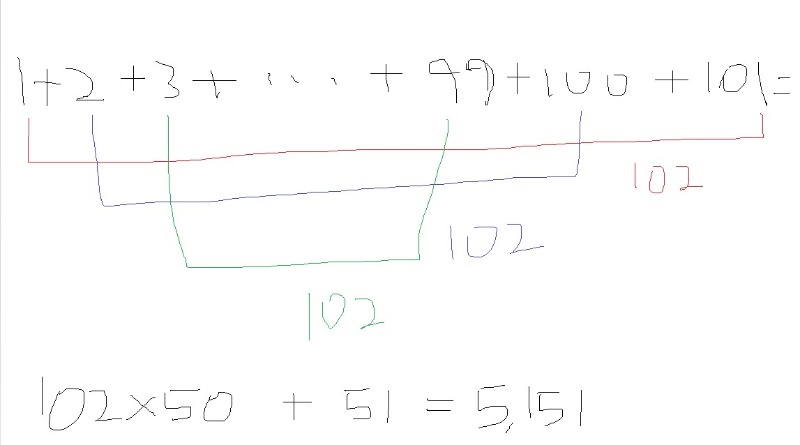
102X50+51을 풀이하면, 102가 50번이 있고, 가운데 남은 51을 더해준다는 의미이지. 처음 풀어보는 방법이라면 조금 복잡할 수 있지만 익숙해지면 하나씩 더하는 것보다 더욱 빠르고 정확하게 계산할 수 있어. 짜증 나는 감정으로 종이를 찢지 않고 이성적으로 구할 수 있지.
또 다른 방법은 없을까? 이런 고민이 바로 수학을 통해 창의력을 기르는 방법이란다. 재밌지..?
너의 웃음에 선생님도 힘이 나는구나. 이런 방법은 어떨까? 다시 1+2+3+4+5 = 식으로 돌아와서, 숫자의 크기를 막대로 표현해보는 거야.
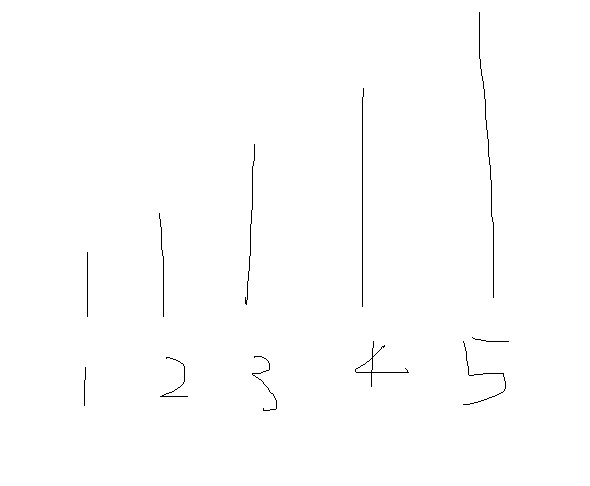
숫자를 다 더한다는 의미는 막대의 길이를 모두 더한다는 의미와 같겠지? 그런데 가만 보니..
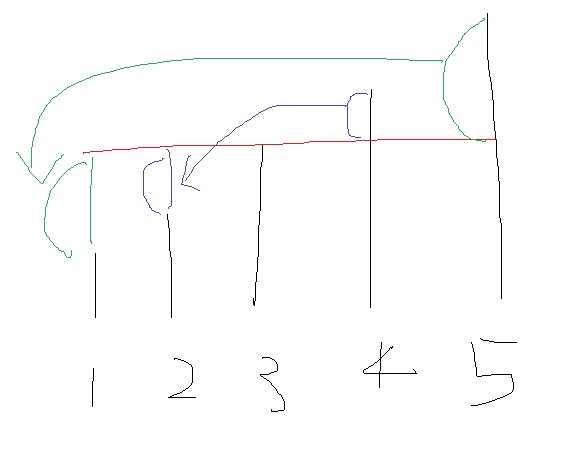
4의 파란 부분을 2로 옮기고, 5의 초록 부분을 1로 옮긴다면? 다음 그림이 되겠구나.
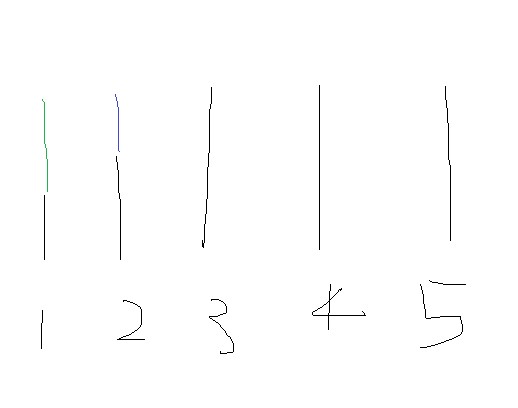
숫자의 합은 막대 길이의 합을 구하는 것과 같다고 했지? 그렇다면 위 그림에서 식을 어떻게 세울 수 있을까?
그렇지! 3 X 5라고 세우면 되겠지? 중간 길이인 3의 막대를 5번 더하는 것과 같으니까.
이렇게 숫자를 그림으로 표현해서 문제를 해결할 수도 있단다. 이 방법을 이용해서 1+2+3+4+ ... +99+100+101 =를 구해주면 다음과 같이 나타낼 수 있겠지.
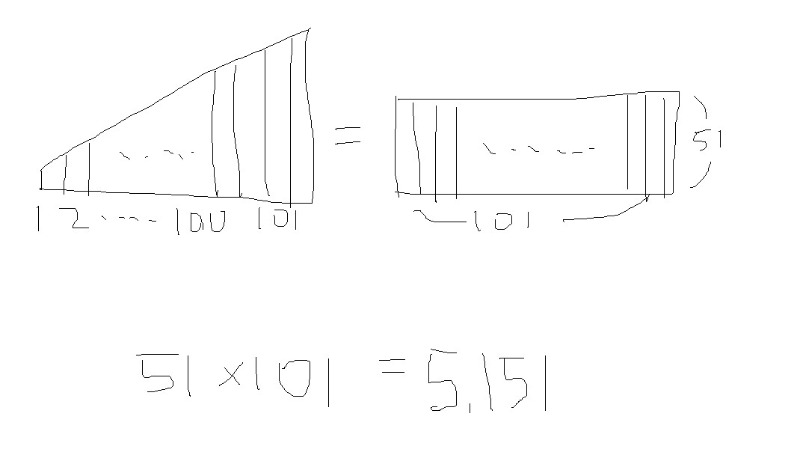
1부터 101까지 막대 길이의 합을 구하는 것은, 중간 길이인 51 막대 길이를 101번 더하는 것과 같지.
어떠니? 1+2+3+4+ ... +99+100+101 = 문제 하나를 가지고 정말 다양한 풀이 방법을 고민할 수 있었지? 물론 선생님이 제시한 풀이 방법 말고도 다른 방법이 있을 거야. 그 방법을 고민해보고 내가 생각한 방법으로 풀었을 때 정답인 기분이란!
***
지금까지 수학 공부하는 이유를 정리해봤다. 논리력과 창의력. 더 복잡해졌다고? 그렇다면 너만의 이유를 찾아보렴. 분명 너의 성장에 도움이 되는 부분이 있을 거니까.


