6학년 수학 배움, 어떻게? - 각기둥과 각뿔
원래 6학년 1학기 수학 첫 단원은 분수의 나눗셈입니다. 그런데, 분수와 소수의 나눗셈을 한 단원으로 묶어 배우기 위하여 이를 뒤로 뺀 후, 먼저 2단원인 각기둥과 각뿔부터 배우려고 생각하고 있습니다.
성취기준은,
[6수02-06] 각기둥과 각뿔을 알고, 구성요소와 성질을 이해한다.
[6수02-07] 각기둥의 전개도를 그릴 수 있다.
입니다.
가만히 보면, 6학년 수학 도형 영역은 도형 감각을 주로 안내하는 것으로 배움이 이루어짐을 확인할 수 있습니다. 아무래도 중학교 도형 영역처럼 고도로 추상화 된 도형 개념을 배우기에는 아이들의 발달 과정 상 어려움이 있다보니, 아이들이 일상 생활에서 만날 수 있는 구체물을 토대로 접근하는 면이 있다고 볼 수 있습니다.
그런 면을 토대로 생각해 볼 때, 교과용 도서의 편제는 아쉬움이 있습니다.
교과용 도서는 단원 도입에 1시간을 할애한 후, 7시간에 걸쳐 각기둥과 각뿔에 대해 배우고 있으며, 나머지 3시간 동안에는 도전수학, 얼마나 알고 있나요, 탐구수학 등의 정리·심화 배움을 구성하고 있습니다.
그런데, 5시간에 걸쳐 배우는 각기둥과 각뿔의 구성요소 및 특징에 대한 부분은 중복 편제되어 있습니다.
각기둥의 구성요소와 함께 높이에 대해 배운 후, 밑면에 따른 각기둥의 종류를 배우고 각기둥이 가진 특징을 배웁니다. 그런 다음 그대로 각뿔에 대해서 같은 방식으로 배웁니다.
제 배움의 아이디어는, 어차피 같은 흐름으로 각기둥과 각뿔에 대해 배운다면, 아예 각기둥과 각뿔의 구성요소와 특징을 같이 배울 수 있지 않을까, 라는 생각에서 시작되었습니다.
그러면서, 기왕 구체물을 토대로 추상화 된 도형의 특징을 배우는데, 구체물을 추상화하는 과정을 조금 더 생각하면서 배우면 좋겠다는 생각을 갖게 되었습니다.
아래는 이러한 생각을 토대로 백워드 설계의 방식을 사용하여 성취기준을 분석하여 배움 내용을 추출한 것.
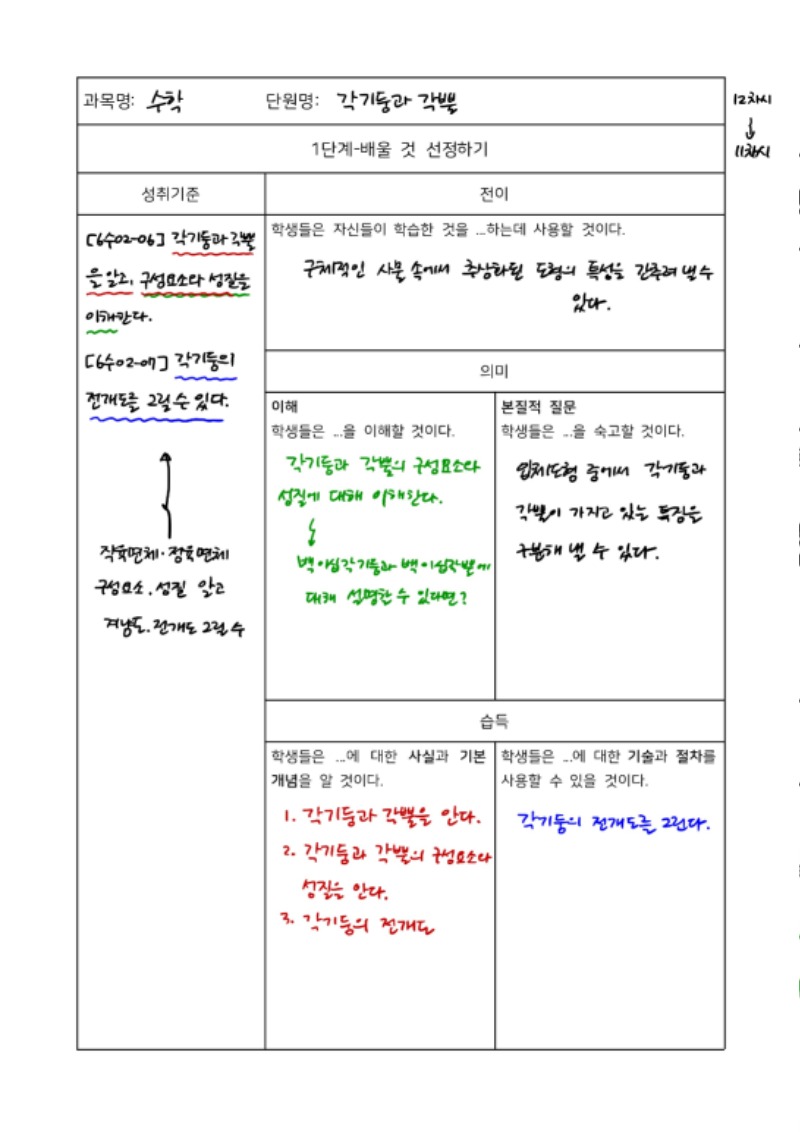
성취기준에는 명확하게 드러나지 않지만, 도형 영역의 본질적 이해는 추상화에 가서 닿아야 합니다.
우리가 배우는 모든 도형은 추상화 된 상태로 우리의 인식 체계 안에 수용되기 때문입니다. 놀랍게도, 우리가 살고 있는 세계 속에서 완벽한 정육면체를 구현할 수 없습니다. 그럼에도 우리는 정육면체를 인식하고 이의 특성을 이해합니다. 도형 영역이야말로 수학이 가진 추상성을 확연하게 드러내는 부분입니다. 그래서 중학교 1학년 수학 도형 영역이 작도를 배움으로 시작되는 것을 이해할 수 있습니다.
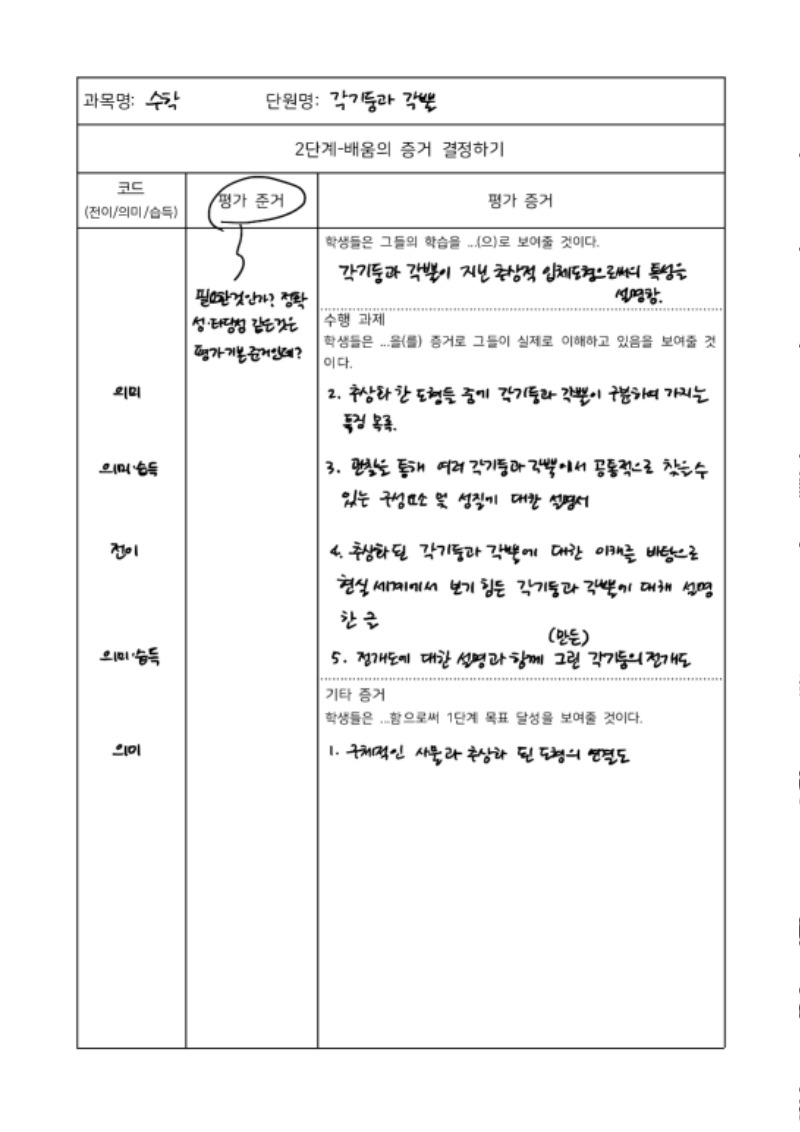
위 템플릿은 백워드 설계 2.0 버전입니다. 평가 준거에 대한 항목이 있는데, 설계를 작성하면서 느끼는 것이지만, 우리나라 환경에서는 사족과 같다는 생각이 듭니다. 굳이 타당성이니 적절성이니 명확성이니 같은 준거를 각 평가 국면에 붙일 필요가 있을까 싶습니다.
현재 초등학교 교육과정 상의 성취기준을 평가와 배움의 국면으로 확장하는데 있어서, 백워드 설계 2.0 버전보다는 1.0 버전이 조금 더 심플하게 접근할 수 있다는 생각이 듭니다. 새로운 것이 항상 옳은 것은 아닐 수도 있습니다.

첫 시간은, 이전까지 배워 왔던, 구체적 사물이 추상화되는 과정을 다시 한 번 되짚으면서 확인해 보고자 하였습니다. 서로 다른 구체물을 추상화 된 같은 도형으로 인식할 수 있음을 통하여, 도형 영역에 대해서는 우리의 사고 속에 '이데아'가 내재되어 있다는 것을 확인하고 넘어갈까 합니다.
두 번째 시간은, 구체물과 추상화 된 도형을 연결한 이전 시간 배움을 토대로, 우리 배움 주제인 각기둥과 각뿔이 가지는 특성을 생각해보고 간추리는 배움 활동을 수행할 생각입니다. 서울 잠실의 롯데월드타워와 서울역 앞 대우빌딩은 분명히 다른 도형으로 추상화되는데, 그 이유는 무엇이며 왜 대우빌딩 같은 건물을 각기둥이라고 부르는지, 혹은 롯데월드타워 건물은 각뿔에 가깝다고 하는데 그 이유는 무엇인지 조금 더 명확하게 밝혀 볼 수 있도록 할 생각입니다.
세 번째 시간은, 각기둥과 각뿔의 종류(?)에 대해 생각하고 이야기 나누어 볼 생각입니다. 삼각기둥, 사각기둥, 오각기둥, ··· 과 같이 다양하게 이름 붙는 까닭을 생각해보고, 이와 같이 나누어지는 다양한 종류의 각기둥과 각뿔 제각각이 가진 특징이 무엇인지 찾아보게 할 생각입니다. 기왕이면 위 예시와 같이 그림도 좀 그리고 하면서 시각적으로 돋보이게 표현해 보도록 안내하려고 하는데... 그렇다고 저걸 하는 방법을 지도하고 싶지는 않습니다. 그건 수학 시간에 안내할, 수학 배움은 아니니까요.

네 번째 시간은, 위 배움을 토대로 이제 추상화 된 방식의 사고를 할 수 있는지를 관찰하는 시간입니다. 현실 세계에서 찾아보거나 만들기 어려운 각기둥과 각뿔을 가지고, 아이들이 추상화한 앎을 토대로 추상적 도형의 특징도 찾아낼 수 있는가를 배우고 알아보는 시간입니다. 이 부분은 잘 못하는 학생이 있을 수도 있습니다. 아이들의 발달 단계가 아직 구체적 조작기에 머물고 있으므로, 어려워하는 학생에게는 조금 낮은 수준의 추가 과제를 부여할 수도 있을 것입니다.
다섯 번째 시간은, 각기둥의 전개도에 대해 알아보게 됩니다. 구체물인 과자 상자를 준비한 후, 전개도는 즉 과자 상자의 겉면을 평면 위에 나타낸 것임을 확인하는 것으로 시작할 생각입니다. 이를 위해서 과자 상자를 자르기 전에 우선, A4 용지에 과자 상자의 겉면을 대고 그리는 활동을 할 생각입니다. 그 후 잘라보면서 확인하고, 더 나아가 굳이 잘라보지 않고, 평면 위에 나타내지 않고 전개도의 넓이를 구할 수 있는지도 물어볼 생각입니다. 물론 각기둥의 겉넓이는 이후에 배우므로 이 정도까지만 확인하여도 될 듯 합니다.
여섯 번째 시간에는, 빈 종이에 전개도를 직접 그린 후 이를 접어 각기둥으로 만들어 보는 배움 활동을 할 생각입니다. 이는 평면도형인 전개도의 구성요소가 입체도형인 각기둥의 구성요소와 매칭되는 부분을 알게 하는 배움으로써 도형의 형태가 바뀌면서 구성요소는 어떻게 바뀌는지를 경험하는 시간이 될 것입니다.
이렇게 배워낸 후, 나머지 시간에는 배움을 확인하고, 확인한 것을 토대로 배움을 심화하거나 보충하는 시간으로 사용할 예정입니다.
교과용 도서는 이렇게 배운 후, 바로 도전 수학과 탐구 수학으로 나아갑니다. 심화 과정을 다루는 것인데... 이렇게 배워도 아직 교육과정 상의 성취기준 중 일정 수준에 도달하지 못한 학생이 분명히 있습니다. 따라서 바로 도전 수학과 탐구 수학으로 나가는 것은 아이들의 완전 학습을 위해서는 그 체계가 부족하다고 생각하고 있습니다.
저의 2020년 수학 배움 설계는,
1. 개념 이해 및 확인
2. 교과용 문제 풀이
3. 문제 만들기 활동
4. 단원평가
5. 문제 만들기 활동 및 단원평가 확인
6. 심화 문제 상황 확인
7. 얼마나 알고 있나요(단원 마무리) 풀이
의 과정으로 진행할 생각입니다. 배움 후 교과용 도서를 함께 풀어보면서 이해 정도를 체크하여 바로 보완한 후, 문제 만들기 활동 및 단원평가를 통해서 다시 부족한 정도에 대해 체크한 후, 단원 마무리 활동을 통해서 부족한 지점을 체크 후 보완하는, 한 단원 안에서 지속적인 배움 확인 및 보완 단계를 운영할 계획입니다. 다만 도형 영역의 배움에는 굳이 문제 만들기 활동을 할 필요까지는 없어서, 이번 단원에는 문제 만들기 활동은 하지 않을 것입니다.
아울러, 교과용 도서 풀기 활동에서는 또래교수를 운영할 생각입니다. 아래는 또래교수 운영에 대한 포스팅.
따라서 나머지 다섯 시간 동안에는 위와 같이 '교과용 도서 풀기 - 단원평가 - 단원평가 확인 - 교과용 도서 탐구 수학 활동을 통한 추상화 확인 - 단원 마무리 활동'을 통해 각기둥과 각뿔 단원의 배움을 마무리 할 생각입니다.
아에드 인 마이오렘 델 글로인