7. 바보야! 문제는 교과서야! [초등교사, 초등수학을 말하다]

초등교사, 초등수학을 말하다
7. 바보야! 문제는 교과용 도서야!
조금 논쟁적인 이야기가 될지도 모르겠습니다.
2015 개정 5, 6학년군 수학과 교육과정 상의 성취기준은 총 50개로 구성되어 있습니다. 5, 6학년 2개년 동안, 어린이들은 총 408시간(초등학교: 40분 1시간, ‘한 차시’라고 말함)동안 50항목에 대해 일정 수준의 성취에 도달하면 됩니다.
각각의 성취기준을 대략 살펴보면, 예컨대 초등학교 6학년 ‘수와 연산’ 영역에는 아래와 같은 성취기준이 있습니다.
[6수01-11] 분수의 나눗셈의 계산 원리를 이해하고 그 계산을 할 수 있다.
그리고 교육과정 문서에서는 ‘분수의 나눗셈은 ‘(분수) 나누기 (자연수)’, ‘(분수) 나누기 (분수)’, ‘(자연수) 나누기 (분수)’를 다룬다.’라는 설명이 부가되어 있습니다. 6학년 1학기와 2학기 동안 두 단원에 걸쳐 분수의 나눗셈 단원이 등장하고 있는데, 대략 스무 시간 동안 아이들은 분수의 나눗셈 계산 원리를 이해하고, 그를 이용하여 계산을 하는 기능을 익혀, 관련 문제를 풀 수 있게 됩니다.
교과용 도서는, 학생들이 성취기준 상의 일정 성취수준에 도달할 수 있도록 만들어진 교재입니다.
제가 발령받던 2010년대 초만 하더라도, ‘교과서’의 진도를 제대로 나가지 않으면 민원이 들어오기도 하였습니다. 학년 말 연수 자리라도 있으면, 교감 선생님이나 학년부장 선생님께서 교과서 진도 이야기를 꼭하시곤 했던 기억이 납니다. 배움의 대상이 교과서다, 라는 생각은 그러나, 지금은 많이 희석되어가고 있습니다.
학교에서는 교육과정 재구성에 대한 요구가 점점 늘어나고 있으며, 이는 필연적으로 교과용 도서의 위치를 이전과는 다른 것으로 만드는데 일조하게 됩니다. 그러면서 자연스럽게 이런 의문을 가지게 됩니다.
‘교과용 도서, 정말 아이들을 일정 성취기준 상의 성취수준에 도달할 수 있게 만들어 주는게 맞아?’
6학년 2학기 1단원 분수의 나눗셈은, 위 분수 나눗셈 중 ‘(자연수) 나누기 (분수)’와 ‘(분수) 나누기 (분수)’의 계산 원리를 안내하고, 이에 대한 기능적 접근 이후에 다양한 연산 문제 및 (소위) 적용 문제를 풀도록 안내합니다.
그런데 그 단원은 각각 다음과 같은 순서로 이루어집니다.
- 동분모 분수의 나눗셈
- 이분모 분수의 나눗셈
- (자연수) 나누기 (분수)의 나눗셈
- 대분수와 가분수의 나눗셈
이를 도식화하면 아래와 같습니다.
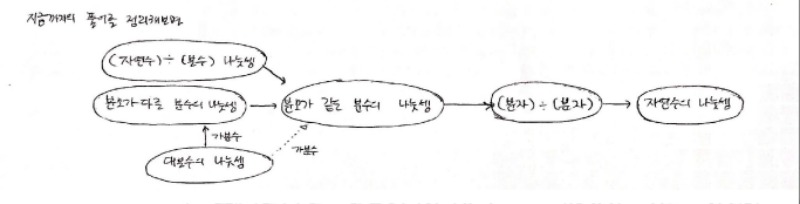
결국, 위 네 유형 다, ‘(자연수) 나누기 (분수)’, ‘(분수) 나누기 (분수)’의 꼴을 ‘(분자) 나누기 (분자)’로 바꾼 후 자연수의 나눗셈으로 형태를 바꾸어 푸는 방식으로 설명하고 있습니다.
교과용 도서는 굳이 분모의 꼴을 기준으로 위계화하여 각각의 차시에서 ‘연습’시키고 있는데, 그러지 말고분수 나눗셈을 푸는 방식이 ‘(분자) 나누기 (분자)’의 꼴로 수렴되며, 이를 이용해 자연수의 나눗셈을 푸는 것임을 충분히 안내한 후, 다양한 국면의 분수 나눗셈을 설명하는 방식이면 더 긴 시간동안 충분히 이해할 수 있지 않을까요?
언제부터인가, 사교육 시장에서 많이 팔리는 문제집의 형식이 ‘유형별’ 형식을 띄기 시작했습니다. 물론, 오랜 수학교재인 ‘수학의 정석’ 시리즈도 유형별 정리가 되어 있지만, ‘정석’은 기본 개념을 유형화한 것이라 궤가 다릅니다. 대부분의 문제집이 굳이 기준을 두어 나눌 필요가 없어 보이는 것까지 ‘유형별’로 정리하고 유사 문항을 만들어 연습시키는 것을 볼 수 있습니다.
사교육 경험을 통하여, 유형으로 연습한 학생들이 유형 외의 문항을 만날 때 당황하는 모습들을 많이 보아왔습니다. 연습은 시키지만 사고하게 만들지는 못하는 유형별 문제집들. 공교육이 아이들을 문제 유형별로 연습시키고 있는 셈입니다.
그러니 교실 수업도 획일화됩니다. 교사는 유형을 소개하고, 유형 풀이를 소개하고, 교과용 도서와 수학 익힘책으로 연습시킵니다. 유형을 못풀면 방법을 소개하고, 방법대로 풀 수 있도록 다시 연습시킵니다.
분수의 나눗셈도 자연수 나눗셈의 방법으로 수렴하며, 소수의 나눗셈도 결국은 자연수 나눗셈의 방법으로 수렴한다는 것을 안내하지 못한 채, 그저 방법을 유형별로 연습시키기에 급급합니다. 교과용 도서를 통해 사고하는 경험을 도통 얻기가 힘이 듭니다.
스토리텔링 요소나, (지금은 없어진) 놀이수학, 도전수학과 탐구수학 등의 요소는, 사고하는 수학을 위한 부분인지, 문장제 문제나 복잡한 문제 등 문제 풀이를 연습하기 위한 부분인지 계속 의문이 듭니다.
6학년 1학기 각기둥과 각뿔 단원의 도전수학은, 막대와 점토로 각기둥과 각뿔로 이루어진 구조물을 만드는 활동을 합니다. 이쯤되면 이건 수학인지 아니면 미술인지 의문이 듭니다. 설마 Steam 교육이라고 말하진 않겠지요? 이 만들기 활동을 통하여, 아이들은 무엇을 얻는 것입니까.
물론, 도형 영역은 아이들이 도형을 조작하며 얻는 무형의 성장도 간과할 수 없습니다. 아이들은 그저 블록을 쌓는 활동만으로도 도형감각을 키울 수 있을지도 모릅니다.
그런데, 원주를 이용하여 트랙의 길이를 구하는 문제쯤 되면, 이는 문제를 위한 문제 이상이 되기 어렵다는 생각도 듭니다. 다행히, 지금은 원주율을 3으로 놓고 풀 수 있도록 교과용 도서에서도 여지가 생겼지만, 2007 개정 교육과정까지는 원주율을 3.14로 놓고 풀었더랬습니다. 2009 개정에서 원주를 이용한 트랙 문제가 나왔었는데, 그 때는 3.14가 3, 22/7, 3.1 등과 혼용되기 시작한 교육과정 시기였습니다. 트랙과 3.14가 섞이면 아이들은 수학 문제 풀기를 포기합니다. 저도 그런 문항들을 평가 문항으로 내기도 했는데, 지금 생각해보면 참 어리석은 일이었다는 생각이 듭니다. 어쨌든.
3.14를 굳이 사용할 일이 없는데도 - 중학교 진학하면 무리수 ‘파이’로 배우고, 이는 더 이상의 연산이 불가능한, 문자로 취급하여 다룹니다 - 혹자는 아이들의 연산력을 위하여 3.14를 유지해야 한다는 이야기를하기도 합니다. 중고등학교만 가도 소수를 활용한 연산도 잘 다루지 않습니다. 그 때 쯤 되면 수의 복잡성은 점점 수준이 낮아지고, 대신 추상화된 수학이 그 자체로 복잡성을 획득합니다. 계산기가 아이들의 스마트폰에 기본 내장되어 있는 시기에, 3.14를 연산하는 연습이 무슨 필요가 있습니까.
몇 년 전부터, 저는 원주와 원의 넓이 배움에서 원주율을 항상 3으로 고정하여 씁니다. 어차피 중학교가면, 3은 ‘파이’로 바뀌고 그 자체를 연산할 일은 없다는 이야기와 함께 말입니다.
왜 애들에게 쓸데없는 연산 연습을 그렇게나 시키는지 도무지 이해할 수 없습니다. 그건 수학적 사고도 아니고, 그냥 사고도 아닙니다. 생각 없이 알고리즘에 수를 꽂은 후 기계적으로 연산하는 것이 수학적 사고라고 한다면... 수학적으로 생각한다는 것이 무엇인지 조금 더 배우셔야 할 필요가 있어 보입니다.
놀이의 요소롤 도입한다고, 말판에 연산식을 넣어 놀이도 연산도 아닌 것을 만들었던 것이나, 수학적 사고는 쏙 빠진 수학 교과서의 스토리텔링은 더 이야기하지 않겠습니다. 수학을 재미있게 하는 것을 수학 외적인 요소에서 찾고자 할 때의 문제점에 대해서는 이제 모든 분들이 다 알게 되었을 것이라고 생각합니다.
교사가 교육과정 상의 성취기준을 기준으로, 교육과정 재구성과 같은 방식으로 아이들의 배움을 설계하고 실행하는 것이 점점 더 확산되고 있습니다. 교과용 도서가 과연, 아이들을 배우게 만드는지에 대한 고민이 필요한 때입니다.
간혹, 우리나라 수학 교육은 1940년대의 아이디에에서 머무르는 것이 아닐까 싶기도 합니다. 폴리야 G. Polya 교수의 ‘어떻게 문제를 풀 것인가 How to Solve It’를 인상깊게 읽었지만, 이 책이 쓰여지던 당시의 수학에 대한 문제의식과 지금의 문제의식은 사뭇 다르다고 할 수 있습니다. 그러나,아직도 우리는 수학 ‘문제’를 풀려고 애쓸 뿐, ‘수학적’ 문제를 해결하기 위한 모습은 아닌 듯 싶기도 합니다.
교사의 아이디어가, 수학적 사고를 품은 교육과정의 운영으로 드러나고, 학생들로 하여금 성취기준 상의 일정 성취수준에 도달하도록 하면서도, 수학적 흥미와 호기심을 잃지 않으려면, 유형을 버리고, 문제 풀이중심의 과정 운영을 바꾸며, 수학 익힘책의 형식을 수학적 사고를 증진시킬 수 있는 다양하고 엄밀하며 풀이와 정답에 관해 열려있도록 바꾸어야 할 필요가 있다 생각합니다.
아에드 인 마이오렘 델 글로인

