[2009개정 6학년 1학기 수학] 2. 분수와 소수의 나눗셈 01
KimTeacHer
0
1520
0
2018.04.22 14:40
2. 분수와 소수의 나눗셈
01 문제의 의미
원래 교과(용 도)서는 2단원 분수의 나눗셈, 3단원 소수의 나눗셈으로 구성되어 있습니다. 그런데 교육과정 연구를 하다보니, 굳이 이것을 두 단원으로 나눌 필요가 있을까 싶은 생각이 들었습니다. 단원을 하나로 합치면서 내용을 재구성하면, 특히 아이들과 활동하면서 수학을 배울 수 있는 기회가 생기지 않을까 싶었습니다. 그런 계기로 하나의 단원으로 내용을 다시 구성하였습니다.
가장 먼저 '문제의 의미'에 대한 이야기를 해 보았습니다. 오늘의 질문은,
집에서 학교까지 2km의 거리만큼 떨어져 있는 학생이
1분에 1/5km씩 걸어간다고 할 때, 집에서 학교까지 오는데 몇 분이 걸리는가?
의 문제에 대한 식을 세워보는 것이었습니다.
아이들은 쉽게, 식이
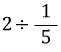
이 됨을 이야기할 수 있었습니다.
그리고, 다음 문제.
9/11m의 노끈을 2/11m씩 잘라 나누어 줄 때, 남은 끈의 길이는 몇 m인가?
를 연이어 제시하였을 때, 아이들의 반응은 바로,
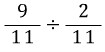
라는 식으로 표현되었습니다.
어떤 아이들은, 많은 아이들의 이러한 반응에 고개를 갸우뚱하는 반응을 보였습니다. 구하라는 것이 얼마나 남았는가인데 왜 나눗셈 식을 세우는가, 라는 의문이었습니다.
가장 강력하게 의문을 제시한 어린이는 학원이나 다른 사교육을 하지 않는 학생이었습니다. 그것이 이번 교수-학습 과정에서 가장 인상적인 부분이었다고 할 수 있습니다. 어쨌든,
이러한 아이들의 답은 앞 문제와 뒷 문제 간 인상효과였을 수도 있습니다. 바로 앞에 전형적인 나눗셈 문제가 나왔는데, 그 뒤에 나오는 문제도 별 의심 없이 나눗셈 문제로 생각하게 되는 것이죠. 그래서 이는 함정문제일 수도 있습니다. 그래서 아이들이 문제의 식을 잘못 이해했을 수도 있지만, 어쨌든,
교사가 가진 의도는 확실하게 전달된 듯 싶습니다. 제시된 식에 대한 의문을 표시하는 몇몇 어린이들 덕택에, 아이들이 문제를 다음과 같이 풀고 있다는 것을 명확하게 확인할 수 있었으니까요.
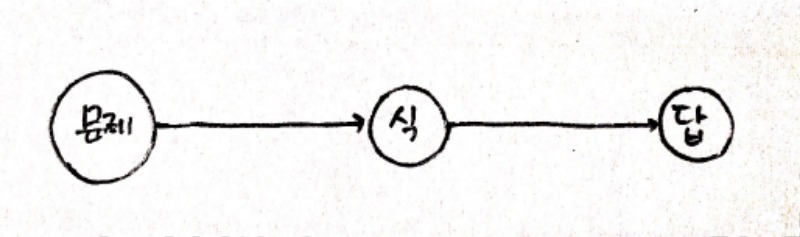
그럼 도대체 어떻게 풀어야 하는가.
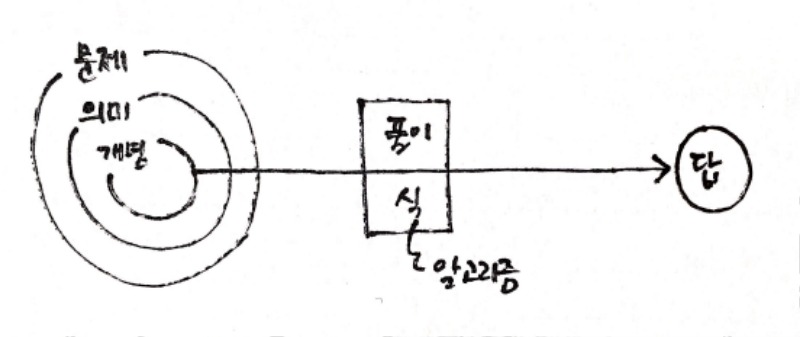
제가 아이들에게 제시한 도식은 다음과 같습니다. 알고리즘 같은 어려운 단어는 빼고. 아이들에게 문제가 나오면 우선 문제를 바로 식으로 옮기지 말고, 문제 속에 숨겨진 '문제의 의미'를 생각해보도록 안내하였습니다. 문제가 가진 의미는 문제와 관련 있는 개념으로 넘어가는 다리 역할을 합니다. 문제의 의미를 포착하지 못한 채, 그저 문제 자체를 가지고 식을 표현하면 제대로 된 풀이를 시작할 수 없게 되며, 올바른 답으로 나아갈 수 없게 됩니다.
그래서 답을 틀리고, 수학에 흥미와 자신감을 잃게 되는 것이죠.
문제가 가진 의미를 생각한다면, 위 두 번째 문제의 식은 나눗셈 식이 아니라는 것을 알 수 있습니다. 뺄셈식으로 구하면 쉽게 구할 수 있습니다.
따라서, 교과(용 도)서 단원 중심의 학습 구조가 또한 얼마나 아이들의 선입견에 중요한 영향을 주는지도 생각해보게 됩니다. 어떤 아이들은 '분수의 나눗셈 단원이니까 당연히 식도 분수의 나눗셈 식이죠'라고 이야기하기도 합니다. (올해는 그런 아이가 없었지만) 문제의 의미에 대해 생각하지 않고, 그저 습관적으로, 인상에 따라서 식을 세우고 풀어서 답을 구하고, 틀리는, 그런 것들에 대한 고민부터 아이들과 함께 나누어 보았습니다.
다음 시간에는, 그렇다면 나눗셈 문제를 풀기 위하여, 과연 나눗셈의 의미는 무엇인가 함께 이야기해 보기로 하였습니다.
아에드 인 마이오렘 델 글로인
[이 게시물은 편집장님에 의해 2018-05-22 23:58:06 자유에서 이동 됨]

